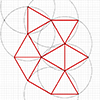
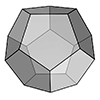
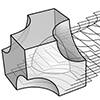
Modeling a rhombicosidodecahedron requires exploding and extending the faces of a dodecahedron and an icosahedron of the same edge length. We begin with both polyhedra centered at the same point. Then, we explode the faces of the dodecahedron and icosahedron outward from the center. We extend their planes while maintaining their orientation and shape. As these faces extend, they intersect and form new polygonal regions. Triangular and pentagonal faces emerge […]

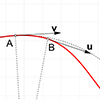
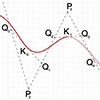
Curvature can be roughly described as how much a curve is “turning” at point a P. We place two “very” close tangents and measure the difference between them. The closer these tangents are, the more precise our approximation would be. An osculating circle is a tangent circle that has the same curvature as the curve at point P. The larger the circle, the more “flat” the curve is. An infinitely […]

Truncation refers to the process of shortening something by removing parts. You can apply truncation to numbers, text, or data in various contexts. A truncated polyhedron is a geometric solid formed by truncating the vertices of a regular polyhedron. Truncation involves cutting off the corners or vertices of the polyhedron in such a way that the original faces become polygons with new edges. This process creates new faces at the […]

The rhombitrihexagonal tiling is one of the semi-regular tessellations. It is composed of regular hexagons, squares, and triangles. It is a periodic tessellation since you can copy the fundamental unit and move it across the plane to generate the tiling. I use this quality of the tiling to draw and expand it in Rhinoceros software. This is a basic drawing exercise. At the same time, it is a nice exercise […]

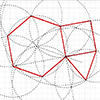
The snub square tiling is one of the semi-regular tessellations, where regular triangles and squares match perfectly to fill the plane without gaps or overlaps. The Euclidean construction of Snub Square tiling is possible by utilizing the basic compass and straightedge operations. I made this construction in Rhinoceros to show that there is no need for any numerical input to locate the points and draw the tiling. There are two […]

Villa Savoye is an iconic modernist villa in Poissy, France, built between 1928 and 1931. It was designed by the pioneering Swiss-French architect Le Corbusier, often considered one of the most influential architects of the 20th century. Villa Savoye is a masterpiece of the International Style, embodying the principles of modern architecture that prioritize functionality, simplicity, and the use of new materials such as reinforced concrete. I made this digital […]

This is a 3d modeling tutorial for the platonic solid of dodecahedron. Modeling a dodecahedron is a good exercise for the basic transformation commands such as Rotate3D in Rhinoceros. You will see that it is possible to calculate the rotation angle by using sphere intersections. I learned this elegant method while teaching Architectural Geometry classes 12 years ago. It is based on the fact that, given a rotation axis and […]

This is a short video tutorial on the B-Spline decomposition I studied earlier here. This tutorial demonstrates how to decompose a B-Spline curve into Bezier curves using Rhino. Despite the original Bezier-de Casteljau algorithm requiring degree+1 control points, Rhino allows drawing a degree-3 curve with any number of control points. By examining knot points and dividing segments appropriately, the B-Spline curve can be manually subdivided into Bezier curves. This involves […]

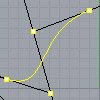
In this short tutorial, I am going to show you how to locate a parametric point on a Bezier curve. This will be a third-degree cubic Bezier curve. So, I start by placing four control points. I name these points from P0 to P3. Then, I connect them by a polyline in order. I explode the polyline into the segments. The parameter of my point must be a number between […]

“Mihr-î Mah” in Ottoman Turkish translates to “The Sun and The Moon” in English. She was the most powerful imperial princess in Ottoman history according to historians. The Mihrimah Sultan Mosque is located in Üsküdar district of Istanbul. It was built for Mihrimah Sultan, the daughter of Kanuni Sultan Süleyman and Hürrem Sultan. It is one of the early works of the architect Mimar Sinan. Sinan supported the main dome […]

Here is the method I used for approximately modeling the Gyroid, a triply-periodic minimal surface. It is very popular in architecture because the symmetrical solids and voids it generates are interesting. I modeled this for the Common-action Wall project we exhibited together with Fulya Akipek in 2017. After several attempts to generate it in Grasshopper, I decided to model it in Rhino. There are some sources on the internet, explaining […]

While digging through the lecture archive, I found this video I made in 2017. We introduce Platonic solids and Archimedean solids in the Design Geometry course at Istanbul Bilgi University. This video shows how we can create an Archimedean solid, the Truncated Tetrahedron, by folding it from a flat sheet.While doing this, I intersected the spheres by using the relations between the side lengths of the solid, and I calculated […]

The Parquet Deformation named “Wiry Wonder” was designed by Michael Cuttita in William Huff’s studio at the State University of New York in 1989. The below figure shows the original drawing made by the student. Similar to the previous one, this composition is based on a hexagonal lattice. In this composition there are three significant prototiles, marking the three key moments in the shape-shifting process. There is also one invisible […]

“Strange Start Startling Stop” was designed by Mary Purdy at the State University of New York in 1985. The composition is based on a hexagonal lattice (above figure). There are four prototiles, marking the four key moments in the shape-shifting process. The first prototile is a regular hexagon, which is also the first tile of the composition. This prototile morphs into a shape that is a composition of four smaller […]

I realized this method of constructing basis splines from given control points while searching for a way to teach students about basis splines. I couldn’t find an easy and visual method to create clamped basis splines by connecting simple cubic Bézier spans. It is a tough job and requires lots of complex equations. However, I suddenly realized that there is a special way of doing that. So I decided to […]

Below is a simple tutorial class we studied in Rhino in 2015 and 2016. The exercise is called “A Low-Poly Habitat”. The aim is to create simple polygon models by analyzing the overall geometric topology of an animal body. First-year design students attended the exercise and they are encouraged to create these models using blueprints from www. They used simple commands such as point, line, and surface from 3 or […]

Exercising the “folding” process of a nine-faced solid. Start from its net, and analyze the matching edges. Then, use sphere intersections to calculate the rotation angles. Visit here for more information about this solid: http://aperiodical.com/2013/10/an-enneahedron-for-herschel/

This video is dedicated to Design Computing and Basic Design students, who “contour” and then move each section by hand in Rhino. They do it individually to fabricate their laser-cut homework from cardboard. It could also be a macro but I prefer this. Because it does not work in all conditions. Maybe you should orient your contouring results similar to those shown in the video, and then use the shear command […]

It is Baldequin (or Baldachin) in English, Baldeken, or Baldöken in Turkish. I don’t know which one is correct, but it is the name of a structural system of arches and pendentives that carry a dome. Sinan experimented with square, hexagonal, and octagonal variations in his mosque designs (as I developed parametric definitions of them in my 2003 master thesis (here)). Today, together with students we’ve modeled the system and […]

Lokma is the name of a pastry made of fried dough soaked in sugar syrup or honey and cinnamon, typically shaped into a ring or ball. Unfortunately, it is not the “Lokma” we’ll study here. In Turkish, there is another meaning of the same word related to the history of Eastern architecture. It is the name of metal connectors in railings, mostly inside of the openings of garden walls and […]