While reviewing past Grasshopper studies, I stumbled upon a Parametric Muqarnas study dating back 11 years. Although it shares numerous characteristics with a muqarnas design, it is not a perfect match. The Grasshopper definition used in that study was not particularly efficient, prompting me to revisit and improve it. This particular design presents various challenges, making it an excellent exercise for mastering Grasshopper. My goal with this study was to […]

The interlocking frame structures represent a quintessential example of parametric design since very old times. More recently, they gained widespread attention through the Metropol Parasol in Seville, captivating architects and designers. I’ve extensively explored these structures on this blog, attempting various methods like manual slit drawing and solid/region boolean operations. My latest iteration aimed for greater simplicity and adaptability on complex surfaces. I call this new version Interlocking Pavilion. The […]

Archimedean Solids are convex polyhedra with faces of regular polygons and vertex-transitive. There are 13 such objects (excluding prisms and antiprisms which are probably less exciting). In this study, I experimented with these solids and designed a family of planters. Since they are convex and look cool, I decided to give it a try. I call this algorithm Archimedean Planters. The first part of the definition deals with the generation […]

“In the heart of a sunflower’s embrace, its seeds weave a poetic tale—a dance of two spirals, parastichies they’re called. One unfurls gracefully from the center in the hush of clockwise whispers, while its counterpart whispers secrets in the tender breaths of counterclockwise motion. A subtle ballet unfolds, where the number of these spirals gracefully mirrors the whispers of adjacent Fibonacci numbers, composing a delicate symphony in the sun-kissed fields.” […]

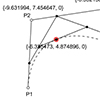
Today’s curve is the beautiful Bezier curve. A series of linear interpolations between the coordinates of control points describe a Bezier curve. So, I created a simple tool in Grasshopper called Bezier Function Extractor to experiment with this elegant construction. In the linear form (degree 1) the linear interpolation between 2 points (P1 and P2). The point at parameter t (0<= t <= 1); Q = tP1 + (1-t)P2. In […]

This week’s fractal is the famous Dragon Curve. Dragon Curve exhibits self-similarity, meaning parts of the curve resemble the overall shape, regardless of scale. It’s fascinating because a relatively simple construction process generates a complex and visually captivating fractal pattern. The Dragon Curve is often used to demonstrate fractal properties in mathematics and is popular in recreational mathematics due to its intricate and beautiful patterns. It has applications in computer […]

Here is a simple pavilion design I call the Turtle Pavilion. It was exceptionally easy. The planar shapes placed on the sphere continue to be planar after the ellipsoidal deformations. I was amazed when I first noticed this, for some reason. With Grasshopper’s Facet Dome component, we can panel spheres as we desire. When we deform these panels in the X, Y, and Z directions, they continue to remain planar. […]

The Polyhedra Unroller with Flaps is a simple tool I developed for the obvious purpose. It picks any polyhedra (closed polysurface) from the user and unrolls it flat on the XY plane. This part is easy because a short Python script is sufficient. The important function of the script is the generation of the production drawings from the unrolled net. It means, the generation of the flaps. Here, the continuous […]

The Weaire-Phelan structure is an optimal solution to the problem of partitioning space into equal volumes with the least surface area. Denis Weaire and Robert Phelan discovered it in 1993. This structure gained attention due to its efficiency in filling space, offering a configuration that achieves a more balanced distribution of volume and surface area compared to other known structures at the time. Here is my model for Space-filling Weaire-Phelan […]

In this study, I explore Cesaro Fractal, generated by Grasshopper. Usually, it is not possible to code recursive algorithms in Grasshopper. With the help of the Anemone add-on, these fractal curves are easy to model. I studied similar fractal algorithms here before. This one is very similar to the Koch’s snowflake. The only difference (as far as I understood) is the side of the spikes. Koch’s Snowflake generates triangular spikes […]

Here are the variations of classical six-pointed star patterns generated by Grasshopper. Generally, you can see these patterns under the title “Islamic patterns” because they are frequent in the decorations of mosques and palaces. I studied these patterns in Grasshopper earlier in these posts. I always find this an interesting geometry exercise. This time, my main goal was to develop a useful code only with the native Grasshopper components that […]

Perlin noise is a gradient noise function that has been widely used in computer graphics, procedural generation, and various other applications to generate natural-looking patterns. Here is my brief exploration of the Perlin Noise Generator. Although I didn’t fully follow the traditional steps the result looks similar. I started with the square grid and generated random gradient vectors on every grid corner. Then, I implemented the original algorithm’s dot product […]

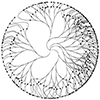
This Grasshopper exercise is a special one. I used Hoopsnake components to develop the branching design I studied earlier here. This time I multiplied the number and orientations of several tree structures to generate my interpretation of the Tree of Life. The challenging part of the algorithm was to finalize every branch tangent to a predefined circle. Group 3 handles this issue by utilizing a Blend Curve component. There are […]

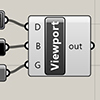
Recently I found this VB.net component in an old Grasshopper project. I am not sure if it is mine or not, but I wanted to share it with you. This code modifies Rhino viewport colors quickly without entering the Rhino options window. I frequently modify the viewport colors and grid settings to create renders or animations within Grasshopper. This is why, this component might be useful in making quick modifications […]

In this short trial, I will be testing the Open Nest add-on for Grasshopper. The add-on is available in food4rhino as of 2023. For this test, I will use the latest exercise on Interlocking structures I experimented with here. Nesting is an important topic, especially in today’s economic crisis. It reduces the waste materials on laser-cut plates. First, I should re-visit the interlocking structures Grasshopper definition here. The below image […]

Here is a short tutorial on getting help from Grasshopper in physical terrain modeling. It is a classical architectural terrain modeling process. Let’s see how Grasshopper can help us with this. Part 1: Terrain modeling for Laser cutter The terrain model entered in the Brep data store in this application is a closed/solid model. For now, you can also use ready-made components such as Cone or Sphere (Sph) to quickly […]

Let’s have some fun with the parametric stuff! You may remember that we created many vases and glass alternatives that we could bake with a single Revolution (RevSrf) component in previous exercises. Since we were referencing the profile curve drawn in Rhino, it was also possible to create a one-component glass algorithm with some Rhino knowledge. Now, we will try to develop a parametric mug. In the application you see […]

In this short tutorial, I want to give Grasshopper beginners the basics of how we create attractor systems. The Grasshopper definition you see in the below figure is the equivalent of array-type copying operations in CAD. However, unlike in CAD programs, here we are dealing with multiple generations of objects rather than transformations. Attractor Basics: Data Matching In the application you see in the figure below, each row of the […]

I have created a straightforward Grasshopper code that generates a Voronoi diagram on a surface. Then, it adds thickness to form a structure called a “Voronoi Cage.” In the initial step, I project a surface onto the ground plane (Z=0). The projected frame serves as the boundary for two operations: generating random points using the Populate 2D (Pop2D) function and calculating the Voronoi diagram based on these points. The resulting […]

This is an update on my 2012 exercise on rhombille tiling. This reminded me of the old-school subdivisions of surfaces again after 11 years. It was while reading about rhombic dodecahedron (the stackable solid), that I came across this cute tiling. It’s quite simple, just a hexagonal grid with a special reconstruction. I decided to recreate it by using well-known native Grasshopper components. I animated the result with a variation […]