An octahedron is a polyhedron and platonic solid with 8 faces of identical equilateral triangles. In this post, I will try to explain the drawing and unrolling process of the octahedron. It has a close relationship with the cube as it’s dual. In order to construct an octahedron, we first have to create a square. The main problem of drawing the square is determining the right angle (perpendicular axis) to […]

[2011_12_25_divide] here is the fundamental of surface subdivision in Grasshopper. In order to design a parametric truss exercise, this is the generally accepted starting point. Get a surface from the file, subdivide it into U and V directions to create point lists, and then manipulate these points to create something interesting. Having a list of points would also present good potential regarding attraction with other entities, such as point or […]

I am learning Grasshopper. In this Circle Crossing definition, I tried to create the above pattern (also described in Sunflower Spiral) as simply as possible, this definition creates not only spirals but is also capable of more tessellations I guess. Maybe a three-dimensional equivalent might be studied in the future. As you can see from the definition, I started with a large circle. Then, I divided it into segments and […]

This time, in order to develop a potential “dummy” surface for Grasshopper experiences, I built a better definition. The Graph Surface definition uses a polygon as a basis, divides the edges and moves them according to various parameters. It’s fun to play with mapping different graph types and various polygons and subdivision values. Surprisingly, this definition led me to a wide range of possibilities I haven’t planned. Especially, shifting the graph […]

Recording History in Rhinoceros3D has interesting potential. You might utilize it in the process of design exploration. We’ll try to show its concept and limitations; First, build two surfaces; one is planar at the world XY plane, and the other represents the “initial” form of your design. Put another surface on the planar one, as if it’s an ideal “component” of the finished geometric composition. Activate the “Record History” button […]

NURBS surfaces by nature, like four-corner topologies with U and V directions. Şebnem Yalınay Çinici has formulated a tectonic exercise of “Primitive Hut”, which in my point of view is a tough geometric challenge; a subdivision on a real three-corner manifold. That seems very easy at the beginning as both Rhinoceros and Grasshopper are able to create surfaces with three corners, by either lofting, meshing, or edge curve methods. However, those […]

This experiment is based on a traditional surface-component definition. However, the variation of components is associated with Gaussian curvature. We just control the subdivision and a multiplier value. Results are interesting in as an educational tool to explain NURBS surface curvature and its utilization for Design Geometry. Different surface shapes generate exciting results. Of course, this could be much improved by recognizing positive and negative curvature values, (probably only accepting […]

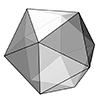
Icosidodecahedron is an Archimedian Solid, a thing in between the Platonic Solids of Icosahedron (d20) and Dodecahedron (d12). It is a rectified version of an Icosahedron, constructed by dividing every edge into two equal segments and joining these segments to create a composition of equilateral pentagons and triangles. Archimedian Solids consist of at least two equilateral polygons, whereas Platonic Solids are constructed by only one. We’ll deduce an Icosidodecahedron from […]

Sunflower Spiral (or Phyllotaxis) can be constructed in Grasshopper according to Vogel’s model of parametric relationships. This model uses polar coordinates. You can download the Grasshopper definition file here: (The Grasshopper file is still working after more than 11 years -15.12.2022. This is such a powerful quality of Grasshopper, I think.) It’s a good example of utilizing polar coordinates. It’s also fun to play with the parameters and constraints of […]

We’ll use the “Animate” function in Grasshopper3D to create a stop-motion animation. First, you need to determine the parameters you’ll animate, which means defining maximum-minimum values of it. In our example, we’ll be using a simple bezier curve generation algorithm. You can download it here [2011_12_21_bezier curve.ghx]. In this definition, we plan to animate one parameter which is the value of “t” between 0.0 to 1.0. This single change affects various […]

Today’s polyhedra is the beautiful icosahedron. It is one of the five Platonic Solids with twenty equilateral triangular faces. Its dual is the dodecahedron, which has pentagonal faces. Here, I explained the process of modeling an icosahedron. After creating a regular pentagon, you should find the “tip” point of the Icosahedron by intersecting spheres from at least three of the corner points with a radius of the pentagon’s edges. You […]

A truncated Tetrahedron is an Archimedian Solid, created by slicing a Tetrahedron. Its faces are regular hexagons and triangles. Assuming you’ve created a Tetrahedron, first join its faces to create a polysurface. Now, you may re-create the lines of Tetrahedron’s edges, either by drawing them or generating them (Curve/Curve from Objects/Duplicate Edge). While the edge lines are selected, hit (Curve/Point Object/Divide Curve By/Number of Segments) and type 3 to create the […]

This is a semi-regular tessellation of vertex arrangement 4.8.8. Its octagonal and square forms are all generated from data lists provided by the new version of subdivide component (The old one was processing points in a different fashion. I don’t know why they changed that). Anyway, a lexical operation is needed to convert this list into a more useful one for this exercise. You can download the source definition here […]

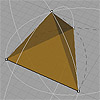
The tetrahedron is a platonic solid with 4 equal triangular faces (which are also equilateral), 6 equal edges, and 4 vertices. While creating this shape, we will take a closer look at length transfers using compass-like tools both in two and three-dimensional space. In order to define the edge length of the first triangle (which is a straight line), start with any two points in cartesian space. Using a compass […]

The smooth and continuous nature of the “Sine Surface” has garnered significant popularity among designers and architects alike. This captivating curved surface offers a visually pleasing aesthetic that adds an elegant touch to various design projects. Its flowing contours and gentle undulations create a sense of harmony and organic beauty. Recently, I delved into this with the help of Grasshopper’s Graph Mapping functionality, I began my artistic journey. Although I […]

Design scripting is initially based on secondary syntactic mechanisms that control sequential executions of code. We call this model of computation control flow programming. On the other hand, dataflow represents a widespread alternative to control flow by utilizing concurrent streams of data. Dataflow programming languages are also considered as pedagogical tools in fields where the coders are not expert computer programmers. In the last decade, new parametric modeling tools introduced […]

This is my first post in designcoding, dated 14.11.2011. I revisited the code and decided to re-publish it in 2024. Hello World! This is the Emergent Polygons definition, one of the first Grasshopper studies I made while learning the language. This is a very efficient programming language for designers and architects since it utilizes geometric relationships very intuitively. I think it will be more popular and widely used in the […]