The poincare disk is still an interesting representation of hyperbolic space for me, full of mysteries. I’ve had several attempts to understand it previously (here and here). Finally, I found a resource* explaining basic concepts about it. I tried to repeat some of the constructions in Rhinoceros, (without any logical purpose). The most important part is the conversion of a Euclidean point into a hyperbolic space. There is no clear […]

Previous studies on the timer component were based on understanding its use. This time, I tried to implement it in a geometric design task. Moreover, manipulating the timer component to change the regular animation of parameters. Time does not have to be equally divided into sequences. Rather, new possibilities may emerge with different time flows. A simple triangulation system is developed with a potential manipulation, based on a timer. This […]

We can model a musical composition using native Grasshopper components. After the experiments with the timer component (here and here), I managed to build a definition that allows us to produce outputs in various time intervals. I converted a small part of Bach’s Bouree in E-Minor into Grasshopper as a guitar tablature. I used Guitar Pro 5’s MusicXML export function to convert classical guitar tablature into XML data, then organized […]

[GHX:0.8.0066] Here is today’s improvement on my metronome with the timer component, which started here. It’s straightforward to tell Grasshopper about seconds and organize it according to it. Using an interval smaller than 1 second, this small script catches every second and returns a different value. However, it’s much harder to implement smaller values than seconds. It seemed easy at first sight but getting accurate results smaller than seconds requires working […]

This was before Spherical Fantasies, while I was trying to update my surface equation definition. In between designerly intentions and mathematical facts, it’s hard to maintain a process, while keeping the definition yet simple and open to exploration. Grasshopper definition is here: [GHX: 0.8.0066] A little tired of mathematical definitions, I started to give names to the animate surfaces I develop. Like the Spherical one, this is also a trigonometric equation […]

This is about conforming distortions on surfaces and creating imperfect (say ugly) surfaces. I started with planar surfaces, however, I continued with spherical ones. There are interesting results when applying trigonometric functions to spherical surfaces. Example surface equations: W=(sin(x*y)) / 2 and W=(cos(x)+sin(x-y²)) / 2 Please be patient if animations are loading slowly. But they represent a way of creating free-form-looking surfaces, highly mathematical behind the scene. Here is the […]

This is probably the most simple definition on this site but I think it’s very useful. The timer is a special component of Grasshopper that is significant in terms of the real-time sketching paradigm. This basic use of a timer includes a 1-second update to a Vb script. Inside the script, the system date’s seconds are returned, so we see a real-time increasing number at output A. Beyond this point, […]

The Truncated Icosahedron (5,6,6) is an Archimedean Solid we often recognize as the iconic soccer ball. This geometric structure, also affectionately known as the “Buckyball” in honor of the visionary architect Buckminster Fuller, has gained significant popularity and recognition both within the realms of mathematics and everyday life. It is composed of twelve regular pentagons and twenty regular hexagons, meticulously arranged to achieve a harmonious balance. This symmetrical nature makes […]

Truncated hexagonal tessellation (or named 3-12-12) is represented in hyperbolic space (as far as I understood it). The idea is simple if you don’t mix it with complex equations. Below is the 2-dimensional representation of hyperbolic projection. Paper space is defined by the thick line there. Projection is based on a two-sheet hyperboloid surface. Euclidean version of this tessellation is described here. Here is the Grasshopper3D file containing the above […]

[GHX: 0.8.0066] This is my second attempt on getting into non-euclidean representations of space. Althouth it seems easy at first sight, this represents a close point of theory between mathematics and contemporary computational design geometry. As always, architects tend to use mathematical terms such as “non-euclidean geometries” but as far as I saw, most of them have no idea about what it is. So, I’m trying to learn and understand this […]

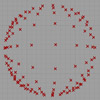
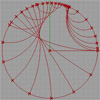
This is my first attempt at representing a non-euclidean space. There are several representations of a non-euclidean space in euclidean means such as Beltrami-Klein or Klein, Poincare, Poincare half-plane, and Weierstrass. Here, I tried to understand Poincare’s approach. Random straight lines are drawn on a hypothetical hyperbolic space using a simulation of Poincare’s famous disk representation. Although there is a precise description of the disk and its construction, I used a ready-made […]

Using SPM Vector Components developed by two talented people, Daniel Hambleton and Chris Walsh (website here), I’ve studied ways of displaying dynamic diagrams of form. I’ve modified an example file and found myself in a surprising formal exploration. It’s like watching the clouds, giving them meaning like a sheep, a flower, a baby… Here is a link to the Grasshopper file. Right-click and save it to your computer (don’t left-click it) [GHX: 0.8.0066: SPM […]

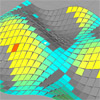
I’ve worked a little more about the Solar Position definition I’ve started here. The definition uses Danel da Rocha’s beautiful solar position script and utilizes it with other components. It creates visual output for any given surface, divided into quads (with side faces of course) and coloring according to their orientation to the sun. This time (file here: [GHX: 0.8.0066]) I added an occlusion part to calculate the surface’s own shadow. Now, […]

Here I am testing the nesting. RhinoNest is a plug-in for Rhino and a set of components for Grasshopper. I tested it using my old interlocking fabrication definition (here) and (here). I downloaded RhinoNest from this website and installed it. However, I sounded a little complicated at first sight. Then I found a sample definition (here) and modified it a little bit to meet my purposes. First of all, I added orientation components […]

I have come across several high school topics I was afraid of. While I was searching for a geodesic dome definition in Grasshopper, it was quite surprising that I found an easier way of modeling an approximation of icosahedron, the famous platonic solid. Icosahedron was a research topic of this website at various posts before (here, here, and here). In order to generate geodesic spheres, first I had to solve […]

Yesterday, Kağan asked me about the isovist component in Grasshopper and how it works. In fact, it is a long story, I said because once upon a time, I was curious about Space Syntax theory as my old friend Ela Çil introduced it. So, here is an original definition of Michael Benedikt; “The environment is defined as a collection of visible actual surfaces in space. An isovist is the set […]

Creating and handling new types of grid configurations might be an important topic, as Grasshopper is not supporting them natively (yet). I tried to create some semi-regular tessellations based on regular grids. It is actually truncated versions of regular grids, but it slowly becomes interesting as I realized that I may further truncate emerging grids to create Level 2 and Level 3 grids with more complex tessellations. Here are two […]

Not all of them, but when you get the idea, you’ll see there are lots of different alternatives for creating Fuller’s famous Geodesic Domes (Although in fact, he is not the inventor of it). I was playing with Platonic Solids in Rhino and realized that the “Pull” command is very useful in subdividing objects. I modeled this in Rhino 4. First, take a regular Icosahedron and divide it. Because, this […]

Playing with the 2D Metaball component in Grasshopper. I was curious about why there are no Metaballs in 3D in Grasshopper. Then, I realized that in fact, the 2D Metaball component is creating a section of a 3D Metaball computation. I think it is a topic worth studying even 10 years after this original post to develop an easy way to create the metaball surfaces. In 2012, thanks to the […]

Basic Design Studio at Bilgi University is coming to semester’s big final. Nowadays, students are trying to build their final projects. Oğuz and Gupse’s group has a truss structure with nearly 800 segments. They attempt to build it by taking length values from their own Rhino model by hand. And this itself had brought a difficulty, because one person of the group should be assigned only to do this measurement, […]