Can we go back to the beginnings of algorithmic design tools, when it was still as simple as possible (not to the binary level of course)? Most of the theorists agree about the fact that contemporary parametric design tools sometimes provide needlessly many possibilities that suppress the designer’s own creativity. The Voronoi component in Grasshopper was one of the cult examples of that (mentioned here). Throughout this blog, I always […]

Last year, I posted a way to create a Grasshopper command button in Rhino 4 (here). As the scripting possibilities increase in Rhino 5, the new tab feature can be used to put them together. I’ve made 4 of the most used platforms in a tab named “Scripting”. Here is how I did it; Use right-click on the empty area to open the above menu and select “new tab” to […]

I’ve been searching for a method to study the Voronoi subdivision in order to manipulate it. There are well-known algorithms for that. But I thought it would be better if I use a projective approach just as I did in studying hyperbolic space (here). This is the metaphor of inflating balloons. However, I inflated cones instead of spheres. This way, it became possible to modify the algorithm. So I was […]

Today’s Architectural Geometry course was about platonic solids and different attractor objects in introducing component-based design systems. Benay’s idea was both pedagogical and interesting to test in Grasshopper. I searched for the most fundamental type of attractor solid in creating a composition such as this; There is a subdivided sphere and an attractor sphere. The pull component works great here. You may use multiple attractor solids or different shapes such […]

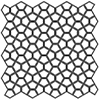
In this exercise, we asked students to develop a method to produce custom tessellations. This is based on the analysis of what is called “Islamic patterns”. We have discussed Eric Brough‘s famous book “Islamic Geometric Patterns”, regarding geometric relationships and linear connectivities via underlying tessellations (such as regular square and hexagonal). Thus, this geometry and drawing exercise is called “Seamless Patterns” in the Design Geometry course at İstanbul Bilgi University. […]

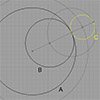
The first-year Architectural Geometry course includes Euclidean constructions as a study of associative geometry. We have exercised the below questions to study this topic. These are three mutually tangent circles, that can be drawn using only a compass and ruler, without built-in tangency functions in Rhino. Such exercises are expected to improve students’ reasoning. We believe architectural geometry education should encourage a conception that allows students to think about what […]

The Möbius strip is a famous mathematical object. Although being in three-dimensional space, it is a closed-loop of only one surface and only one edge. This quality alone makes the object an interesting study for computational design. I aimed to create an object to test our new CNC machine. I wanted to test the egg-crate interlocking fabrication method. This is why the study became a Möbius strip fabrication. Apart from […]

This is not to explain the method of the Parquet Deformation but to see the potential. After we’ve studied regular, semi-regular, dual, and truncated tessellations with students, the Architectural Geometry course expects them to develop a Parquet Deformation handmade such as those shown below. I call them Parquet Deformation handmade. Because they are manually designed but drawn using traditional CAD. The samples you see below are from this website. It […]

This is a late update for my 2012 study on Cairo Pentagonal Tiling (or Cairo Tessellation). Originally, it was an exercise of dual tessellations. Because this tiling is the dual of the famous semi-regular tessellation of Snub Square. After coding the Snub Square tiling, I attempted to generate the dual of it. However, that created an inefficient result. This latest version generates the original Snub Square and Cario Pentagonal Tilings. […]

Here is the step-by-step generation of the old Snub Square Tiling. Frankly, this is the first step in the generation of Cairo Pentagonal Tiling I generated with Grasshopper earlier. Because Cairo pentagonal is the dual of a snub square. The first step was easy. Just dispatch cells of a square grid, then evaluate them according to the ratio of 0.366 approx. which is derived from the bisector of an equilateral […]

The intricate harmony of the Islamic Patterns is amazing. The geometry of this and other Islamic pattern designs are explained in the 3rd chapter of Craig S. Kaplan’s Ph.D. dissertation. I constructed a semi-regular tessellation, particularly the 4.8 because it seems to open interesting explorations that mostly emerge from truncated squares. We know equilateral triangles and hexagons are also fundamental shapes for this task. However, the dual nature of the […]

This was my old plan to work with images in Grasshopper. Certainly, that was not the result I expected, but this could be counted as a starting point. After seeing beautiful circle packing compositions here, I decided to program Grasshopper, so that it’ll create a subdivision, based on image data. This was the initial version, just subdividing a plane with Voronoi points and visualizing it according to the image’s color […]

Today’s fractal is the famous Mandelbrot Set. The Mandelbrot set is a well-known and complex mathematical set often associated with fractals and chaos theory. Named after the mathematician Benoît B. Mandelbrot, it’s a set of complex numbers defined by a simple iterative process. The Mandelbrot set is an intricate and self-similar boundary, which reveals increasingly complex patterns at different magnifications. On the other hand, I heard the term “The fingerprint […]

Today’s fractal is the Julia Set, the amazing simplicity of chaos. There are lots of applets and articles on the internet about this fractal. You can generate this with the iteration of a basic function many times and placing points on the complex plane. I developed a Grasshopper implementation in 2012. Also, this was my first study on complex numbers. At each iteration, the detail level increases. I utilized a […]

Yes, Revit revolutionizes the design process if you get used to it’s interface; but there are lots of things that could be further developed. Representational qualities, for example seems to be an important issue. I use section-perspectives a lot but still there are anti-aliasing problems when you get to the printing process. The last project I developed bottom-up in Revit and printed the posters from it, without any photoshop. This […]

After a couple of days of studying the mysterious Doyle spiral, I’ve decided to test an approach of circle packing from conformal mapping. First, I tried to understand the Poincare disk (earlier at here, here, and here and here). I used it as the hyperbolic representation of space on a two-dimensional plane. Then, I linked a regular hexagonal grid and rebuilt it after the hyperbolic distortion. This led me to find […]

This is a detailed wooden casement window, created for a restoration project last year by Tuşpa Architecture. Revit is used in creating the survey and restitution projects. This component is partially parametric, you can define width and height values. It took about three days to complete the component, way much more than just drawing it in Autocad, but it was very educational for me. You can download and play with […]

I’ve been working on a multi-function building for a design contest. This led me to the custom component designs also. Here is a quick column object with several parameters. You can right-click and download the file here: [RFA: Revit 2012] This was an interestingly easy and quick process of creating a parametric component in Revit. It is somehow similar to Grasshopper3D, with just single revolve command, connected to the variables. […]

I’ve been carried away by a design competition since 10 days. This is a multi-function building with 20.000 m2 floor area. This is the first time I’m trying to design such a large space completely in Revit Architecture. Below are two small modifications I’ve made to meet Turkish annotation standards. Especially the elevation tag is very different from original Revit component. Room tag is also modified because the multi-function buildings […]

We can create tessellations of outer points in a Poincare Disk, using the manual method explained in the last post (here). But repeating that compass and straightedge process is becoming a little useless after a couple of repeats. If you say “ok. I understood the concept, let’s get faster!” then we can model just the same process in Grasshopper3D to examine varying results in seconds; If we connect any grid of […]