This is the continuation of my previous study on the Fibonacci lattice on a spherical surface, creating a Fibonacci Dome structure. The panelization of curved forms with flat surfaces has been a favorite topic in architectural geometry.  The trigonometric layout of the Fibonacci sequence generates a spherical formation, while the Faceted Dome component handles planarity. Here I further enhanced the previous code into a pavilion design. The essential part of […]

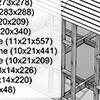
This work emerged out of necessity. In the design and application process of wooden frame structures, where we put thousands of pieces together like a puzzle, the issue of preparing and updating quantity and measurement lists requires the most effort. Hours spent on this and the possibility of making mistakes are very high. However, with the Quantity Surveyor I developed in Grasshopper, you can generate measurement lists almost in real-time. […]

The regular dodecahedron is one of the five Platonic solids, characterized by having 12 regular pentagonal faces, 20 vertices, and 30 edges. When you elongate it, you extend its structure in one or more directions, resulting in a shape that retains the basic properties of the dodecahedron but is stretched out. The elongated dodecahedron might not catch your eye at first—it’s just a long version of a shape you’ve probably […]

Today’s computational curve is the beautiful Sierpinski Triangle. It is a fractal named after the Polish mathematician Waclaw Sierpinski, who described it in 1915, though it had been previously described by other mathematicians. It is a self-replicating pattern that arises from a simple recursive process. To construct the fractal, you start with an equilateral triangle and then repeatedly remove smaller equilateral triangles from its interior, leaving holes. Each iteration involves […]

The rhombic dodecahedron is a polyhedron with twelve rhombus-shaped faces, where each face has four sides of equal length. It is possible to construct the space-filling variant of the rhombic dodecahedron by arranging multiple such rhombic dodecahedra in a regular pattern so that they fill space without leaving any gaps. In his 1611 work on snowflakes titled “Strena seu de Nive Sexangula,” Johannes Kepler observed that honey bees utilize the […]

Lissajous curves, named after the French physicist Jules Antoine Lissajous are a family of curves that emerge from the interaction between two harmonic oscillations. They have applications in various fields including physics, engineering, and signal processing. They are commonly used in electronic devices such as oscilloscopes to visualize the phase relationship between two oscillating signals. Similarly, they are also useful in mechanical engineering for analyzing and designing mechanisms that involve […]

Geodesic refers to the shortest path between two points on a curved surface. It is based on the principles of geodesy, which is the science of measuring the Earth’s shape. On the other hand, in architecture and design, a geodesic dome is a spherical or hemispherical structure consisting of a network of geodesic lines (great-circle arcs) forming triangles. Therefore, the dome’s framework provides strength and stability, distributing stress throughout its […]

Stellated polyhedra are three-dimensional geometric shapes formed by extending the faces of a regular polyhedron (a solid with flat faces) beyond their original boundaries until they intersect with each other. The term “stellate” comes from the Latin word “stella,” meaning star and these polyhedra often have a star-like appearance due to their extended faces. They are popular because of their aesthetic qualities. I studied these forms many times before. This […]

In 2016, archi-union architects and fab-union intelligent engineering completed the renovation of the art gallery in Shanghai, China. The distinctive feature of the building was the robotic masonry fabrication of the brick facades. The undulating and waving parametric bricks were increasingly becoming popular after the introduction of parametric design tools such as Grasshopper and the works of Gramazio & Kohler at ETH Zurich since 2008, I guess. I made two […]

Catalan Solids are the duals of Archimedean Solids. They were first described by mathematician Eugène Charles Catalan in the 19th century. There are 13 Catalan solids, and they exhibit interesting symmetries and unique characteristics. While coding the vertex coordinates of these solids in Grasshopper, I made a simple lamp design to exercise the programming language. The code generates the 13 Catalan Lamps with flaps. Since the polyhedra have planar faces, […]

While reviewing past Grasshopper studies, I stumbled upon a Parametric Muqarnas study dating back 11 years. Although it shares numerous characteristics with a muqarnas design, it is not a perfect match. The Grasshopper definition used in that study was not particularly efficient, prompting me to revisit and improve it. This particular design presents various challenges, making it an excellent exercise for mastering Grasshopper. My goal with this study was to […]

The interlocking frame structures represent a quintessential example of parametric design since very old times. More recently, they gained widespread attention through the Metropol Parasol in Seville, captivating architects and designers. I’ve extensively explored these structures on this blog, attempting various methods like manual slit drawing and solid/region boolean operations. My latest iteration aimed for greater simplicity and adaptability on complex surfaces. I call this new version Interlocking Pavilion. The […]

Archimedean Solids are convex polyhedra with faces of regular polygons and vertex-transitive. There are 13 such objects (excluding prisms and antiprisms which are probably less exciting). In this study, I experimented with these solids and designed a family of planters. Since they are convex and look cool, I decided to give it a try. I call this algorithm Archimedean Planters. The first part of the definition deals with the generation […]

“In the heart of a sunflower’s embrace, its seeds weave a poetic tale—a dance of two spirals, parastichies they’re called. One unfurls gracefully from the center in the hush of clockwise whispers, while its counterpart whispers secrets in the tender breaths of counterclockwise motion. A subtle ballet unfolds, where the number of these spirals gracefully mirrors the whispers of adjacent Fibonacci numbers, composing a delicate symphony in the sun-kissed fields.” […]

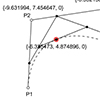
Today’s curve is the beautiful Bezier curve. A series of linear interpolations between the coordinates of control points describe a Bezier curve. So, I created a simple tool in Grasshopper called Bezier Function Extractor to experiment with this elegant construction. In the linear form (degree 1) the linear interpolation between 2 points (P1 and P2). The point at parameter t (0<= t <= 1); Q = tP1 + (1-t)P2. In […]

This week’s fractal is the famous Dragon Curve. Dragon Curve exhibits self-similarity, meaning parts of the curve resemble the overall shape, regardless of scale. It’s fascinating because a relatively simple construction process generates a complex and visually captivating fractal pattern. The Dragon Curve is often used to demonstrate fractal properties in mathematics and is popular in recreational mathematics due to its intricate and beautiful patterns. It has applications in computer […]

Here is a simple pavilion design I call the Turtle Pavilion. It was exceptionally easy. The planar shapes placed on the sphere continue to be planar after the ellipsoidal deformations. I was amazed when I first noticed this, for some reason. With Grasshopper’s Facet Dome component, we can panel spheres as we desire. When we deform these panels in the X, Y, and Z directions, they continue to remain planar. […]

The Polyhedra Unroller with Flaps is a simple tool I developed for the obvious purpose. It picks any polyhedra (closed polysurface) from the user and unrolls it flat on the XY plane. This part is easy because a short Python script is sufficient. The important function of the script is the generation of the production drawings from the unrolled net. It means, the generation of the flaps. Here, the continuous […]

The Weaire-Phelan structure is an optimal solution to the problem of partitioning space into equal volumes with the least surface area. Denis Weaire and Robert Phelan discovered it in 1993. This structure gained attention due to its efficiency in filling space, offering a configuration that achieves a more balanced distribution of volume and surface area compared to other known structures at the time. Here is my model for Space-filling Weaire-Phelan […]

In this study, I explore Cesaro Fractal, generated by Grasshopper. Usually, it is not possible to code recursive algorithms in Grasshopper. With the help of the Anemone add-on, these fractal curves are easy to model. I studied similar fractal algorithms here before. This one is very similar to the Koch’s snowflake. The only difference (as far as I understood) is the side of the spikes. Koch’s Snowflake generates triangular spikes […]