In large-scale projects, calculating tiling layouts for wall, floor, and ceiling surfaces becomes even more critical. Evolutionary optimization of tilings is a viable approach. Considering how time-consuming and labor-intensive this process can be, I considered using Galapagos, an old but often overlooked feature in Grasshopper, which might be particularly useful here. Galapagos provides an alternative interface for evolutionary optimization within Grasshopper. It works by minimizing or maximizing a fitness value […]

Although it appears simple, Goldberg Polyhedra in Grasshopper became a tough challenge, which I like. I spent about 24 hours attempting to generate these. I started with Goldberg’s original method. This creates an equilateral triangle using coordinates denoted as m and n on a hexagonal grid. Then, we place this triangle onto the faces of an icosahedron. Finally, we project them onto a concentric sphere. We can create many polyhedra […]

The Hilbert Curve is one of the results of David Hilbert’s vision of mathematics as a network of symbolic systems. Defined in 1891, this curve is a fractal that fills a two-dimensional plane with a one-dimensional line in the limit. It exhibits self-similarity. It emerged from representing higher-dimensional spaces through continuous, lower-dimensional entities. A curve that grows within a bounded area remains continuous but non-differentiable. Yet it possesses infinite length. […]

I had been researching Goldberg Polyhedra for a while. While exploring how to perform chamfer operations in Grasshopper, I found some interesting results. I want to share them with you. In this Grasshopper project, I reused my previous work, where I built a dodecahedron using the golden ratio. Essentially, all I did was add the Fillet Edge component. I don’t use this component much, so I learned it through this […]

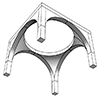
Robotic EarthCrafts II occurred in the summer of 2024 at Istanbul Bilgi University, seven years after the first. Together with Fulya Özsel Akipek, Nilüfer Kozikoglu, Abdullah Mallah, and Halit Mallah, we experimented with the robotic fabrication of molds for rammed-earth structures. The focus shifted toward a human scale based on the experience gained from Robotic EarthCrafts I. At the workshop’s core were spatial systems resembling muqarnas, which incorporated non-planar geometric transitions. Unlike the first workshop, […]

ASCII art is a graphic design technique that uses characters from the ASCII (American Standard Code for Information Interchange) set to create images, symbols, and designs. This form of art involves arranging text characters to form a visual representation of objects, scenes, or abstract patterns. I first encountered this art form in the 90s through readme text files and computer games. Years later, attempting to automate it in Grasshopper was […]

Holger Strøm designed the famous IQlight system in 1973. After more than 50 years, it is still a popular, innovative, and smart design. The IQlight is a self-assembly lamp composed of interlocking quadrilaterals. By utilizing polyhedral geometry, you can generate various shapes and sizes. I created a model of one of the most common IQlight designs, fitting it onto the Catalan solid known as the rhombic triacontahedron. This solid is […]

A pendentive is an architectural feature used in domed structures. It is a triangular section of a sphere that allows for the transition from a square or polygonal base to a circular or polygonal dome. Pendentives curve upward from the corners of the base and support the dome above. They help distribute the dome’s weight more evenly and enable the construction of a dome over a non-circular base. I created […]

Today’s polyhedra are the famous Archimedean Solids! I created a simple Grasshopper script to generate pendants from these beautiful solids. I call this Archimedean Pendants. However, you can implement other polyhedra to the same code. I hardcoded the vertex coordinates so you won’t need an extra add-on to generate the polyhedra. Thanks to the new SubD component Multipipe, it makes life much easier to produce 3dprint-ready results. To make this […]

Urban Atölye, led by architect Nilüfer Kozikoğlu initiated the development of this Grasshopper code. The concept was to create a random relief pattern on a surface to be carved out using CNC technology. In Turkish, this technique is referred to as “kaşıklama,” as the resulting shapes resemble those carved out by a spoon. Consequently, I named this Grasshopper definition “spooning.” The definition employs the Populate Geometry component to achieve a […]

The Image Sampler has always been a very effective Grasshopper component. Once again, I had the opportunity to use this component for a professional job. As you can see, with the help of a straightforward and short script, we can create a relief of an image to fit the desired panel dimensions on the screen. We can process this onto a suitable material using a CNC mill, laser cutter, or […]

Here is a wave generator code I developed using Grasshopper and Python. While searching for a solution to the realistic water simulations, I came up with the Gerstner Waves. I tried to implement it. However, I came up with this final result, which is not a Gerstner Wave generator, but a much simpler one. It combines many user-fed wave components and calculates the resulting single wave. I played with this […]

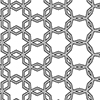
A Penrose tiling exemplifies a type of tiling known as aperiodic. In this context, tiling involves covering a plane with non-overlapping polygons or shapes. Aperiodic means the tiling lacks arbitrarily large repeating sections. These tilings derive their name from mathematician and physicist Roger Penrose, who extensively studied them during the 1970s. Despite their absence of translational symmetry, Penrose tilings can exhibit both reflection symmetry and fivefold rotational symmetry. I created […]

It is not possible to cover a double curvature surface with planar quads. Here is one method that overcomes quad tiling on double curvature by pulling one vertex of the quads to the plane defined by the other three. This method was used in architecture on several occasions such as the exterior facade of The Yas Hotel, designed by Asymptote Architecture in 2009. The same approach is also evident in […]

Today’s beautiful curve is the spherical cycloid. It is a cycloid, rolling on a 3d circular path rather than a straight and 2d one. There are algebraic explanations of this curve. Therefore, I find it interesting to experiment with them, since it is more interesting than the regular planar cycloids, epicycloids, and hypocycloids. This curve is believed to have been studied first by Jean Bernoulli in 1732. The interesting and […]

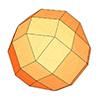
An Archimedean solid is a convex isogonal (vertex-transitive) and nonprismatic solid that is composed of two or more regular polygonal faces. There are thirteen such solids in geometry. Coding the snub dodecahedron study aims to generate one of these solids, composed of 12 regular pentagons, and 80 regular triangles. You can generate the snub dodecahedron by expanding and twisting the faces of a dodecahedron outward. This also creates rhombicosidodecahedron, which […]

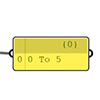
In this short tutorial, I am showing the essentials of data domains in Grasshopper. A domain is a data type in Grasshopper that represents a portion of the 1d or 2d number space. This requires a starting and ending point in those spaces. In 1d, these points are two numbers. Then, the domain represents all the numbers between them. In 2d, a data domain is represented by two coordinates (u, […]

In 1986, Craig Reynolds developed an algorithm aiming to model the flocking behavior of birds, which remains a cult method used in flock simulations today. In my initial study, the bird-oids (boids) have no rules or limitations, just chilling randomly on the screen. I call this initial version Wandering Simulator. There are several reasons why this fundamental simulation is difficult in Grasshopper and Python, our parametric design interface. In Grasshopper […]

Here is a method for coding the dodecahedron and all its irregular variants in Grasshopper as quickly as possible. I utilized the golden ratio rectangles, usually used to construct the sister polyhedron, the icosahedron. However, the magic component of the Grasshopper, the Faceted Dome rescued me again to generate the dual of it, the dodecahedron. This is a special platonic solid, which has 12 regular pentagonal faces. There are several […]

This is the new version of my previous study on the deformation of Islamic Patterns. I love the purity and simplicity of the geometric construction processes of these patterns. It is possible to observe them in many places in many different forms. By continuing this work, I aimed to highlight the pattern deformations that map out all the variation possibilities of these patterns. Unlike previous versions, this time I aimed […]