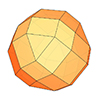
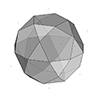
Although it appears simple, Goldberg Polyhedra in Grasshopper became a tough challenge, which I like. I spent about 24 hours attempting to generate these. I started with Goldberg’s original method. This creates an equilateral triangle using coordinates denoted as m and n on a hexagonal grid. Then, we place this triangle onto the faces of an icosahedron. Finally, we project them onto a concentric sphere. We can create many polyhedra […]
Posts categorized under Tools and Languages
The Hilbert Curve is one of the results of David Hilbert’s vision of mathematics as a network of symbolic systems. Defined in 1891, this curve is a fractal that fills a two-dimensional plane with a one-dimensional line in the limit. It exhibits self-similarity. It emerged from representing higher-dimensional spaces through continuous, lower-dimensional entities. A curve that grows within a bounded area remains continuous but non-differentiable. Yet it possesses infinite length. […]
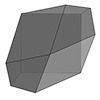
I had been researching Goldberg Polyhedra for a while. While exploring how to perform chamfer operations in Grasshopper, I found some interesting results. I want to share them with you. In this Grasshopper project, I reused my previous work, where I built a dodecahedron using the golden ratio. Essentially, all I did was add the Fillet Edge component. I don’t use this component much, so I learned it through this […]
Robotic EarthCrafts II occurred in the summer of 2024 at Istanbul Bilgi University, seven years after the first. Together with Fulya Özsel Akipek, Nilüfer Kozikoglu, Abdullah Mallah, and Halit Mallah, we experimented with the robotic fabrication of molds for rammed-earth structures. The focus shifted toward a human scale based on the experience gained from Robotic EarthCrafts I. At the workshop’s core were spatial systems resembling muqarnas, which incorporated non-planar geometric transitions. Unlike the first workshop, […]
3D printing, also known as additive manufacturing, is a process of creating three-dimensional objects from a digital file by building them layer by layer. Unlike traditional manufacturing, where the material is cut or molded into shape, 3D printing adds material in successive layers. This allows for greater precision and the creation of complex geometries. In this short tutorial video, I am using Cura software to slice a simple geometry for […]
Relief in the context of art and sculpture refers to a technique where a three-dimensional form is created on a flat surface. The object or figure “protrudes” from the background, creating depth and texture. In this short tutorial video, I am modeling waves relief using the basic drawing and modeling commands of the Rhinoceros software. Here, I use the point surface command. Because, in Rhinoceros, generally we describe the parametric […]
Truchet patterns refer to a set of geometric designs based on simple, repeating shapes, usually tiles or squares. These tiles can be rotated or flipped to create complex and visually interesting patterns. A French mathematician, Michel Truchet introduced these patterns in the 1970s. Since then, you can see them often in art, design, and mathematics. In this short video tutorial, I am modeling truchet relief in Rhinoceros CAD software. My […]
A “hypar” is short for a hyperbolic paraboloid, a double-curved, saddle-shaped surface often used in architecture and structural design due to its unique geometric properties. It is a ruled surface, meaning it can be constructed entirely with straight lines, despite its curved appearance. In this short tutorial video, I am building a beginner-level 3D pattern that resembles the hypar surface. This is a basic drawing exercise to control the viewport […]
In art, design, and geometry, folding involves bending or creasing a material—such as paper, fabric, or other flexible substances—into defined shapes or patterns. Folding techniques can also be used to create multidimensional forms and structures, blending artistic expression with practical functionality. In this short tutorial video, I am modeling a folds relief pattern. This pattern stands out due to its resemblance to a collapsible folding system, combining both structural and […]
In geometry, a truncated icosidodecahedron, rhombitruncated icosidodecahedron, great rhombicosidodecahedron, omnitruncated dodecahedron, or omnitruncated icosahedron is an Archimedean solid. It is one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces. In this short tutorial, I am constructing an irregular truncated icosidodecahedron. It is not the regular Archimedean solid, but a rough approximation of it. I made this model to exercise the exploration of […]
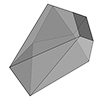
The sphenoid hendecahedron is a unique and interesting polyhedron. As the name implies, a “hendecahedron” is a polyhedron with 11 faces, while “sphenoid” refers to a specific type of shape that is often unusual, asymmetrical, and typically wedge-shaped. This polyhedron fills space, packing 3D space without gaps or overlaps. Its convex shape allows it to tessellate efficiently. Therefore, space-filling polyhedra play a crucial role in understanding tessellations and geometric arrangements, […]
The rhombicosidodecahedron, an Archimedean solid, is one of the 13 convex polyhedra made up of regular polygons. While all its faces are congruent, they consist of various types of regular polygons. I previously explored this fascinating polyhedron and am revisiting it now as part of the Architectural Geometry course. In this short tutorial video, I demonstrate the modeling of a rhombicosidodecahedron. Despite its lengthy and unusual name, this polyhedron is […]
The Herschel nonahedron is a canonical polyhedron whose skeleton is the Herschel graph. It has 11 vertices, 18 edges, and 9 faces. Of the edges, 6 are short and 12 are long. It is characterized by having nine faces (hence the prefix “ennea” meaning nine in Greek). In this short tutorial video, I am folding Herschel’s enneahedron. To do that, I am constructing the interior angles of this polyhedron using […]
In geometry, the excavated dodecahedron is a star polyhedron that looks like a dodecahedron with concave pentagonal pyramids in place of its faces. In this short tutorial video, I am modeling an excavated dodecahedron in the Rhinoceros software. I use basic drawing and modeling commands. I aim to introduce this skill to beginner-level architects and designers. As the name suggests, this process includes the construction of the dodecahedron first. Then, […]
A truncated cuboctahedron is an Archimedean solid, meaning it is a highly symmetrical, convex polyhedron with identical vertices and faces of regular polygons. As its name suggests, you can create the truncated cuboctahedron by truncating (cutting off) the vertices of a cuboctahedron. A cuboctahedron is a rectified cube. After you model it, you can divide all its edges into 1/3s. Then, connect those division points to draw the squares, hexagons, […]
An icosidodecahedron is a polyhedron that is part of the family of Archimedean solids. It has 32 faces, consisting of 12 regular pentagonal faces of a dodecahedron and 20 regular triangular faces of an icosahedron. It is highly symmetrical, with the same arrangement of faces around each vertex. In this short tutorial video, I am modeling and unrolling an icosidodecahedron. This polyhedron is very interesting and is mostly used as […]
Stellation of polyhedra refers to the process of extending the faces (or edges) of a polyhedron outward to form new, more complex shapes. These new shapes, called stellations, are created by adding extra vertices, edges, and faces that “project” outward from the original polyhedron’s structure. You can create an infinite number of new polyhedral forms, depending on how you extend the faces and edges. In this short tutorial video, I […]
A dual polyhedron is a concept in geometry where two polyhedra are related in such a way that the vertices of one polyhedron correspond to the faces of the other, and the faces of the first polyhedron correspond to the vertices of the second. The process of creating a dual polyhedron is called duality, and it applies to many regular, semi-regular, and some irregular polyhedra. In the case of Platonic […]
The truncated octahedron is an Archimedean solid, characterized by a mix of hexagonal and square faces, and it has a very symmetrical and regular structure. Buckminster Fuller called this solid “Mecon”. The truncation process includes the cutting the edges of a polyhedron. We do this by dividing every edge of the polyhedron into 1/3s. Then, we carefully re-connect these division points to generate new, planar polygons. In the case of […]
Buckminster Fuller used the term “dymaxion” for a variety of his designs, and one of these was the dymaxion map. It was based on the geometry of a polyhedron. While the dymaxion map is more directly related to the icosahedron, Fuller’s work often involved using other polyhedral shapes. One of them is the cuboctahedron. He used this term for various conceptual and practical designs, particularly in the context of his […]