I have created a straightforward Grasshopper code that generates a Voronoi diagram on a surface. Then, it adds thickness to form a structure called a “Voronoi Cage.” In the initial step, I project a surface onto the ground plane (Z=0). The projected frame serves as the boundary for two operations: generating random points using the Populate 2D (Pop2D) function and calculating the Voronoi diagram based on these points. The resulting […]

As the design of free-form architectural surfaces becomes easier, questioning and foreseeing the feasibility of the construction of these surfaces becomes important. Such an inquiry requires sufficient knowledge of architectural geometry besides the knowledge of materials and structural systems. In this article, we present a preliminary example of a guide. It supports the design and production process of building surfaces with different geometric properties is presented. This guide aims to […]

This is a useful tip both to solve some of the problems with custom surface subdivisions, and to explain the uses of parametric surface evaluations (the U, V, W thing) and the practical use of data lists. Step 1: Put your points inside 0,0,0 and 1,1,0 so that the resulting coordinates can easily be converted to U and Vs. In the example, we are putting some random points between 0,0 and […]

This is based on my failure of creating an optimum solution for planar polygonal subdivisions. There is a method called Tangent Plane Intersection (TPI), explained briefly here (sometimes similar algorithms are called “planar remeshing” and  “variational shape approximation”) which is effectively used in the Trada pavilion (here). I tried to implement a similar method using only native Grasshopper components and no recursion, but it quickly became much more complicated than […]

For the last 10 days, I’ve been searching for a proper algorithm for representing surfaces using planar shapes. It is obvious that triangulation is an answer but there is an interesting research topic of planar remeshing using shapes other than quads, hexagons, or any other regular polygons. Especially in computer graphics, such things refer to the optimization of models to decrease the load of GPUs. In the Grasshopper community, this […]

After playing with vector fields in 2d (here) it was quite easy to create a 3d surface deformation. Here is my first experiment on a regular triangular grid’s three-dimensional behavior within a vector space, that includes a point charge of varying z coordinates. That makes field lines escape to a bounding box, instead of a bounding rectangle. Again, you may play with force decay, the number of samples, and the […]

Today’s Architectural Geometry course was about platonic solids and different attractor objects in introducing component-based design systems. Benay’s idea was both pedagogical and interesting to test in Grasshopper. I searched for the most fundamental type of attractor solid in creating a composition such as this; There is a subdivided sphere and an attractor sphere. The pull component works great here. You may use multiple attractor solids or different shapes such […]

I’ve worked a little more about the Solar Position definition I’ve started here. The definition uses Danel da Rocha’s beautiful solar position script and utilizes it with other components. It creates visual output for any given surface, divided into quads (with side faces of course) and coloring according to their orientation to the sun. This time (file here: [GHX: 0.8.0066]) I added an occlusion part to calculate the surface’s own shadow. Now, […]

Experimenting with various plug-ins for solar calculations, I found Daniel Da Rocha’s robust implementation of the solar position algorithm in vb.net. It calculates the solar angle of any place and time. Although it’s written in the old vb.net component, it still works great. I’m trying to create a fast and easy workflow to optimize Grasshopper models based on solar directions. This is done by projecting faces to the solar planes […]

This is the basic form of a surface division, based on curvature. As each point on the surface has a curvature value, this might be used to dispatch those values and see the points at flat and curved parts of the surface. Here is the Grasshopper definition [GHX: 0.8.0066] (Please use right click + save target as to download ghx definitions in this site. Otherwise your browser may try to execute them […]

As far as I understood, it is impossible to physically construct double-curved surfaces from quadrilateral and planar faces. This definition tries to find an optimized alternative to this problem. Any surface, single or double curved, is divided into standard sub surfaces. But this time, those surfaces are treated as planar surfaces, therefore one corner is moved to meet this requirement. The output consists of only planar surfaces ready for fabrication. […]

Nowadays, I found myself back into traditional hand sketching. Several failed attempts on Grasshopper led me back there. NURBS (and Grasshopper) somehow limits our conception of surfaces to four-cornered (or two-directional) manifolds. Although it sounds like limiting our designs, having four-cornered component spaces has still lots of experimental fields for designers. Escher is a cult person, who transforms the euclidean coordinate system to meet his design intentions. There are lots […]

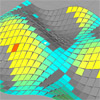
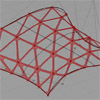
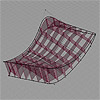
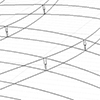
This is the old-method Parametric Truss definition. Interestingly this quickly became a solid solution, used and taught for years. I couldn’t find a better answer yet. As Grasshopper updates, some of the components in this definition change but the overall structure remains. Subdivision of a free-form surface and addition of geometric components has, of course, a wide range of alternatives. Maybe we should combine this with different problems and solutions […]

In this experiment, I’m trying to use data recorder to change components on a surface. The component part is a standart triangular construction, but the attractor points are defined by a 2D slider that is connected to a data recorder. Data recorder remembers last 15 points, while you move the 2d slider, last 15 points are projected on the base surface. This creates an illusion as if a “snake” game […]

A previous work showed a method to create interlocking structures to be created without boolean operations. This time, a small addition is made to create waffle objects using two surfaces, one is the top surface, and the other is the bottom. It was a small modification at the beginning; to replace the “extrude” component with an “edge surface” component. But the interlocking details are now different at each intersection, so […]

The regular component design technique can be further improved by adding several manipulations. The purpose of this study was to create a surface component that reacts to an inherent parameter (actually a geodesic curve on the surface). However, within the process of parametric modeling, diverse formal potentials emerged. Most interesting results are achieved by adding a graph parameter to control the waves of reaction while splitting the surface as stripes. […]

This is a basic formation of component-based design in a dataflow environment. A double-curved surface is subdivided and re-constructed using straight sections. Parametric model of a surface construction by variable components. The main data list of subsurfaces are distributed into four distinct lists, that will be used to construct lines out of double-curved quadrilateral faces. Such definitions could be further advanced by adding a precise fabrication detail. Parametric definition can […]

The cellular canopy is an anonymous tutorial on the history recording capability of Rhino. I’ve been using a “pedagogical” version of this tutorial as an educational tool on the introduction to Grasshopper and Parametric Modeling for architects. The interesting thing with such exercises is they quickly attract students’ attention to the process of designing, in other words, “designing the design process”; is one of the first things we should emphasize […]

There are a couple of experiments in different schools about organizing free-form surfaces (walls here) with a composition of modular elements (bricks). Even though they created robots to make such brick walls, I still couldn’t understand why. Although creating a parametric model that calculates the exact locations of bricks, seems very easy at first sight, there came severe problems to solve in order to achieve a correct layout without using […]

It has been a tough problem for me, for the last two days. A parametric model of an interlocking structure (sometimes also called egg-crate, waffle, or contouring structure) can be created easily in Grasshopper using a Contour component. In addition, you need a couple of list management operations and a boolean (or region) difference event. However, Rhino and Grasshopper are very slow at calculating boolean differences on both solids and […]