Exercising the “folding” process of a nine-faced solid. Start from its net, and analyze the matching edges. Then, use sphere intersections to calculate the rotation angles. Visit here for more information about this solid: http://aperiodical.com/2013/10/an-enneahedron-for-herschel/

This is the Grasshopper definition that generates a tetrahedral helix (also called as Boerdijk-Coxeter helix) but in a funny way. This geometry is also a solution for tangent spheres. I generated the helix using Anemone components for recursion and gave it a little bit of responsiveness. I don’t know if it depends on the speed of your CPU but if it is slow enough, you’ll see the snake game of tetrahedral […]

Lokma is the name of a pastry made of fried dough soaked in sugar syrup or honey and cinnamon, typically shaped into a ring or ball. Unfortunately, it is not the “Lokma” we’ll study here. In Turkish, there is another meaning of the same word related to the history of Eastern architecture. It is the name of metal connectors in railings, mostly inside of the openings of garden walls and […]

Becoming popular after the Beijing 2008 Olympics National Aquatics Centre‘s facade (which is believed to be a Voronoi subdivision, as an epic mistake), the Weaire Phelan structure is a solution of equal volumes with minimal surface area. This nice website briefly explains the phenomenon. There is also an implementation on Grasshopper by Jon Mirtschin. Here, I will be modeling the Tetrakaidecahedron of the Weaire-Phelan structure. First, we define the overall […]

This was a couple of weeks ago, together with my six-year-old son Mete, we decided to make a “ball” out of old memory cards. I was curious about a subdivision method, using only planar quadrilaterals to construct a sphere (named Sixty Square Sphere. There are a couple of models on www. Of course look much better than mine:=). However, my son was expecting a “ball” to play. Then, both of […]

The Truncated Icosahedron (5,6,6) is an Archimedean Solid we often recognize as the iconic soccer ball. This geometric structure, also affectionately known as the “Buckyball” in honor of the visionary architect Buckminster Fuller, has gained significant popularity and recognition both within the realms of mathematics and everyday life. It is composed of twelve regular pentagons and twenty regular hexagons, meticulously arranged to achieve a harmonious balance. This symmetrical nature makes […]

I have come across several high school topics I was afraid of. While I was searching for a geodesic dome definition in Grasshopper, it was quite surprising that I found an easier way of modeling an approximation of icosahedron, the famous platonic solid. Icosahedron was a research topic of this website at various posts before (here, here, and here). In order to generate geodesic spheres, first I had to solve […]

Not all of them, but when you get the idea, you’ll see there are lots of different alternatives for creating Fuller’s famous Geodesic Domes (Although in fact, he is not the inventor of it). I was playing with Platonic Solids in Rhino and realized that the “Pull” command is very useful in subdividing objects. I modeled this in Rhino 4. First, take a regular Icosahedron and divide it. Because, this […]

The tetrahedron is a popular platonic solid for designers. We’ve explained how to draw them using equilateral triangles here before. Recently I’ve found (sorry, lost the web address) a much quicker way of modeling a Tetrahedron using a cube. It’s very simple, just connecting the three opposite corners of the cube automatically makes them equal, resulting in the four equal faces. Of course this time you’ll have to calculate the […]

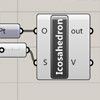
I tried different approaches to drawing platonic solids using Grasshopper’s native components. However, it seems impossible now. In geometric definition, a platonic solid is a set of points, distributed on a sphere with equal distances. If the set contains 12 points, then it’s an icosahedron. I found lots of information about these objects and mathematicians seem to love analyzing them. They created different approaches to building an icosahedron. One of […]

An octahedron is a polyhedron and platonic solid with 8 faces of identical equilateral triangles. In this post, I will try to explain the drawing and unrolling process of the octahedron. It has a close relationship with the cube as it’s dual. In order to construct an octahedron, we first have to create a square. The main problem of drawing the square is determining the right angle (perpendicular axis) to […]

Icosidodecahedron is an Archimedian Solid, a thing in between the Platonic Solids of Icosahedron (d20) and Dodecahedron (d12). It is a rectified version of an Icosahedron, constructed by dividing every edge into two equal segments and joining these segments to create a composition of equilateral pentagons and triangles. Archimedian Solids consist of at least two equilateral polygons, whereas Platonic Solids are constructed by only one. We’ll deduce an Icosidodecahedron from […]

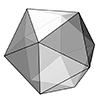
Today’s polyhedra is the beautiful icosahedron. It is one of the five Platonic Solids with twenty equilateral triangular faces. Its dual is the dodecahedron, which has pentagonal faces. Here, I explained the process of modeling an icosahedron. After creating a regular pentagon, you should find the “tip” point of the Icosahedron by intersecting spheres from at least three of the corner points with a radius of the pentagon’s edges. You […]

A truncated tetrahedron is an Archimedean solid, created by slicing a tetrahedron. Its faces are regular hexagons and triangles. Assuming you’ve created a tetrahedron, first join its faces to create a closed polysurface. Now, you may recreate the lines of the tetrahedron’s edges, either by drawing them or generating them (Curve / Curve from Objects / Duplicate Edge). While the edge lines are selected, hit (Curve / Point Object / Divide […]

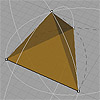
The tetrahedron is a platonic solid with four equal triangular faces (equilateral), six equal edges, and four vertices. In the construction of a tetrahedron, we will look closer at length transfers using compass-like tools in two- and three-dimensional space. To define the edge length of the first triangle, start with any two points in Cartesian space. Using a compass (arc or circle), draw two arches (or circles) using your initial […]