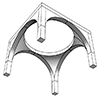
A pendentive is an architectural feature used in domed structures. It is a triangular section of a sphere that allows for the transition from a square or polygonal base to a circular or polygonal dome. Pendentives curve upward from the corners of the base and support the dome above. They help distribute the dome’s weight more evenly and enable the construction of a dome over a non-circular base. I created […]

This is the continuation of my previous study on the Fibonacci lattice on a spherical surface, creating a Fibonacci Dome structure. The panelization of curved forms with flat surfaces has been a favorite topic in architectural geometry.  The trigonometric layout of the Fibonacci sequence generates a spherical formation, while the Faceted Dome component handles planarity. Here I further enhanced the previous code into a pavilion design. The essential part of […]

Geodesic refers to the shortest path between two points on a curved surface. It is based on the principles of geodesy, which is the science of measuring the Earth’s shape. On the other hand, in architecture and design, a geodesic dome is a spherical or hemispherical structure consisting of a network of geodesic lines (great-circle arcs) forming triangles. Therefore, the dome’s framework provides strength and stability, distributing stress throughout its […]

The interlocking frame structures represent a quintessential example of parametric design since very old times. More recently, they gained widespread attention through the Metropol Parasol in Seville, captivating architects and designers. I’ve extensively explored these structures on this blog, attempting various methods like manual slit drawing and solid/region boolean operations. My latest iteration aimed for greater simplicity and adaptability on complex surfaces. I call this new version Interlocking Pavilion. The […]

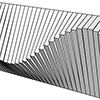
Santiago Calatrava, a celebrated Spanish architect, structural engineer, sculptor, and painter, is renowned worldwide for his groundbreaking and futuristic designs, which frequently fuse architecture with engineering and artistry. Among his many notable works is the door design at Ernsting Warehouse in Coesfeld, Germany, constructed in 1985. I call this Calatrava Door because this design showcases Calatrava’s keen sense of functionality and geometry, with aluminum slats arranged vertically and connected along […]

Euclidean constructions, when represented computationally, rely on algorithms and mathematical principles to generate geometric shapes and forms. Through precise calculations and logical operations, a computer program can emulate the actions of a compass and straightedge, constructing lines, circles, and polygons with accuracy and efficiency. These digital incarnations of Euclid’s timeless techniques enable the exploration of geometric concepts and the creation of visually captivating representations. This project is interesting because of […]

This was my first serious Grasshopper study. In 2009, I decided to attend a design contest for a campus entrance. Of course, the jury didn’t know that the design resulted from a parametric model. I have called this Parametric Entrance since then. The starting point of this project was the conception of the “entrance” as a design problem related to the project area as a whole, rather than just a […]