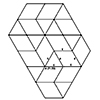
A “hypar” is short for a hyperbolic paraboloid, a double-curved, saddle-shaped surface often used in architecture and structural design due to its unique geometric properties. It is a ruled surface, meaning it can be constructed entirely with straight lines, despite its curved appearance. In this short tutorial video, I am building a beginner-level 3D pattern that resembles the hypar surface. This is a basic drawing exercise to control the viewport […]

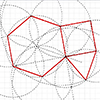
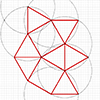
Using a compass and straightedge enables precise geometric constructions, allowing for the creation of complex tessellations. To begin these constructions, a single starting point is sufficient. Circles, which represent a collection of points at a specific distance from the center, and straight lines, which represent a collection of points in a particular direction, are utilized for geometric constructions. In this short tutorial, we move on with the beginner-level drawing exercises. […]

Escher tilings, inspired by the work of Dutch artist M.C. Escher, are inspiring tessellations that cover a plane using repeated geometric shapes without gaps or overlaps. He often used interlocking, recognizable figures like animals and birds to create these patterns, blending art with mathematical precision. His tilings explore symmetry, transformations, and the interplay between two- and three-dimensional space. Escher’s work has influenced both artistic and mathematical fields, particularly in the […]

The term “hexa” generally refers to the number six, derived from the Greek word. It is commonly used in mathematics, geometry, and other scientific fields to indicate six-sided shapes or structures. A hexagon is a polygon with six sides and six angles. It is one of the regular polygons, meaning all of its sides and angles are equal. A hexahedron is a polyhedron with six faces. The most well-known example […]

ASCII art is a graphic design technique that uses characters from the ASCII (American Standard Code for Information Interchange) set to create images, symbols, and designs. This form of art involves arranging text characters to form a visual representation of objects, scenes, or abstract patterns. I first encountered this art form in the 90s through readme text files and computer games. Years later, attempting to automate it in Grasshopper was […]

Urban Atölye, led by architect Nilüfer Kozikoğlu initiated the development of this Grasshopper code. The concept was to create a random relief pattern on a surface to be carved out using CNC technology. In Turkish, this technique is referred to as “kaşıklama,” as the resulting shapes resemble those carved out by a spoon. Consequently, I named this Grasshopper definition “spooning.” The definition employs the Populate Geometry component to achieve a […]

The Image Sampler has always been a very effective Grasshopper component. Once again, I had the opportunity to use this component for a professional job. As you can see, with the help of a straightforward and short script, we can create a relief of an image to fit the desired panel dimensions on the screen. We can process this onto a suitable material using a CNC mill, laser cutter, or […]

A Penrose tiling exemplifies a type of tiling known as aperiodic. In this context, tiling involves covering a plane with non-overlapping polygons or shapes. Aperiodic means the tiling lacks arbitrarily large repeating sections. These tilings derive their name from mathematician and physicist Roger Penrose, who extensively studied them during the 1970s. Despite their absence of translational symmetry, Penrose tilings can exhibit both reflection symmetry and fivefold rotational symmetry. I created […]

It is not possible to cover a double curvature surface with planar quads. Here is one method that overcomes quad tiling on double curvature by pulling one vertex of the quads to the plane defined by the other three. This method was used in architecture on several occasions such as the exterior facade of The Yas Hotel, designed by Asymptote Architecture in 2009. The same approach is also evident in […]

This is the new version of my previous study on the deformation of Islamic Patterns. I love the purity and simplicity of the geometric construction processes of these patterns. It is possible to observe them in many places in many different forms. By continuing this work, I aimed to highlight the pattern deformations that map out all the variation possibilities of these patterns. Unlike previous versions, this time I aimed […]

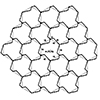
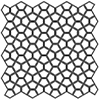
The rhombitrihexagonal tiling is one of the semi-regular tessellations. It is composed of regular hexagons, squares, and triangles. It is a periodic tessellation since you can copy the fundamental unit and move it across the plane to generate the tiling. I use this quality of the tiling to draw and expand it in Rhinoceros software. This is a basic drawing exercise. At the same time, it is a nice exercise […]

The snub square tiling is one of the semi-regular tessellations, where regular triangles and squares match perfectly to fill the plane without gaps or overlaps. The Euclidean construction of Snub Square tiling is possible by utilizing the basic compass and straightedge operations. I made this construction in Rhinoceros to show that there is no need for any numerical input to locate the points and draw the tiling. There are two […]

In 2016, archi-union architects and fab-union intelligent engineering completed the renovation of the art gallery in Shanghai, China. The distinctive feature of the building was the robotic masonry fabrication of the brick facades. The undulating and waving parametric bricks were increasingly becoming popular after the introduction of parametric design tools such as Grasshopper and the works of Gramazio & Kohler at ETH Zurich since 2008, I guess. I made two […]

While reviewing past Grasshopper studies, I stumbled upon a Parametric Muqarnas study dating back 11 years. Although it shares numerous characteristics with a muqarnas design, it is not a perfect match. The Grasshopper definition used in that study was not particularly efficient, prompting me to revisit and improve it. This particular design presents various challenges, making it an excellent exercise for mastering Grasshopper. My goal with this study was to […]

This is an update on my 2012 exercise on rhombille tiling. This reminded me of the old-school subdivisions of surfaces again after 11 years. It was while reading about rhombic dodecahedron (the stackable solid), that I came across this cute tiling. It’s quite simple, just a hexagonal grid with a special reconstruction. I decided to recreate it by using well-known native Grasshopper components. I animated the result with a variation […]

In this short study, I generated Rumi Improvizations. The rumi motif, prevalent in traditional Turkish decorative arts like tilings, window lattices, and fabrics, features a round shape with a comma-like body. Despite resembling stylized leaves, rumis have zoomorphic origins. Rumi compositions depicted stylized animal figures, including birds, lions, deer, fish, and mythical creatures like dragons and Simurg. They symbolized strength, fertility, and the eternal struggle between good and evil. The […]

It has been a while since I didn’t post any patterns. Here is a beautiful one from the iconic design studio of William Huff. Crossover Parquet Deformation is a single-axis, line-based deformation algorithm, constructed on a regular quadrangular hyperframe, designed by Richard Lane at the Basic Design studio of William Huff in 1963. It presents two different parquet deformation sequences linked together. Thus, the designer created a transition between the […]

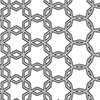
This elegant and straightforward tiling geometry is credited to Dominican priest Sebastien Truchet in 1704 and was documented in a book titled “Memoir sur les Combinasions” (A Memoir on Combinations). After delving into the renowned Truchet Patterns in 2013, I revisited their three-dimensional tiling counterparts today. This served as a valuable exercise in geometry during my previous Design Geometry course. I believe it enhances one’s proficiency in mastering the technical […]

You might recall this type of parametric brickwork from architectural classics, such as the Programmed Wall by ETH Zurich and Gramazio Kohler Research, or the facade of the Mulberry House by SHoP Architects. Initially, I explored the simplest method for placing boxes on a surface, but this approach didn’t yield the correct layout. To improve it, I introduced gaps, which not only liberated the wall’s design but also opened up […]

This is a late update for my 2012 study on Cairo Pentagonal Tiling (or Cairo Tessellation). Originally, it was an exercise of dual tessellations. Because this tiling is the dual of the famous semi-regular tessellation of Snub Square. After coding the Snub Square tiling, I attempted to generate the dual of it. However, that created an inefficient result. This latest version generates the original Snub Square and Cario Pentagonal Tilings. […]