A “hypar” is short for a hyperbolic paraboloid, a double-curved, saddle-shaped surface often used in architecture and structural design due to its unique geometric properties. It is a ruled surface, meaning it can be constructed entirely with straight lines, despite its curved appearance. In this short tutorial video, I am building a beginner-level 3D pattern that resembles the hypar surface. This is a basic drawing exercise to control the viewport […]

This is an update on my 2012 exercise on rhombille tiling. This reminded me of the old-school subdivisions of surfaces again after 11 years. It was while reading about rhombic dodecahedron (the stackable solid), that I came across this cute tiling. It’s quite simple, just a hexagonal grid with a special reconstruction. I decided to recreate it by using well-known native Grasshopper components. I animated the result with a variation […]

Previous studies on trigonometric surface equations showed me an interesting alternative. This is the modification of the breaststroke surface definition. This time, I’m trying to fix the equation and change input values in a fashion that the waves of the surface are not symmetrical. Here are a few experiments on it; (Size, 44.8, X=10, Y=5, animating X’s from 0 to 32) (Size: 42, X=7, Y=5, animating X’s from 0 to […]

You might recall this type of parametric brickwork from architectural classics, such as the Programmed Wall by ETH Zurich and Gramazio Kohler Research, or the facade of the Mulberry House by SHoP Architects. Initially, I explored the simplest method for placing boxes on a surface, but this approach didn’t yield the correct layout. To improve it, I introduced gaps, which not only liberated the wall’s design but also opened up […]

Can we go back to the beginnings of algorithmic design tools, when it was still as simple as possible (not to the binary level of course)? Most of the theorists agree about the fact that contemporary parametric design tools sometimes provide needlessly many possibilities that suppress the designer’s own creativity. The Voronoi component in Grasshopper was one of the cult examples of that (mentioned here). Throughout this blog, I always […]

This was before Spherical Fantasies, while I was trying to update my surface equation definition. In between designerly intentions and mathematical facts, it’s hard to maintain a process, while keeping the definition yet simple and open to exploration. Grasshopper definition is here: [GHX: 0.8.0066] A little tired of mathematical definitions, I started to give names to the animate surfaces I develop. Like the Spherical one, this is also a trigonometric equation […]

This is about conforming distortions on surfaces and creating imperfect (say ugly) surfaces. I started with planar surfaces, however, I continued with spherical ones. There are interesting results when applying trigonometric functions to spherical surfaces. Example surface equations: W=(sin(x*y)) / 2 and W=(cos(x)+sin(x-y²)) / 2 Please be patient if animations are loading slowly. But they represent a way of creating free-form-looking surfaces, highly mathematical behind the scene. Here is the […]

Using SPM Vector Components developed by two talented people, Daniel Hambleton and Chris Walsh (website here), I’ve studied ways of displaying dynamic diagrams of form. I’ve modified an example file and found myself in a surprising formal exploration. It’s like watching the clouds, giving them meaning like a sheep, a flower, a baby… Here is a link to the Grasshopper file. Right-click and save it to your computer (don’t left-click it) [GHX: 0.8.0066: SPM […]

This is another popular “math surface” being rediscovered by designers nowadays, in 2012. Saddle surfaces, seen above as mentioned earlier (here) have a special type named “Monkey Saddle Surface”. This surface was a dramatic example of how Grasshopper can control equations and instantly show graphical results. The mathematical equations start with Z=… this makes it very easy for us to transform any x-y grid centers (a 2d data tree of […]

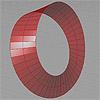
A Moebius strip, also known as a Moebius band, is a fascinating mathematical object and a type of non-orientable surface. It was discovered independently by the German mathematicians August Ferdinand Möbius and Johann Benedict Listing in the 19th century. To visualize a Moebius strip, imagine taking a long, narrow strip of paper and giving it a half twist before connecting its ends to form a loop. The result is a […]

One of the most popular shapes in topology studies is the one-edge, one-face Moebius strip. Here is a basic definition that generates Moebius-like lofted surfaces. I say Moebius-like because, in Grasshopper, Rhino, or any NURBS surface method, I couldn’t manage to model this shape in its real topological singularity. The tricky part of this Grasshopper definition lies at the end, as I take the first segment of the surface, flip […]

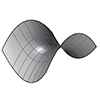
Since the mid-20th century, the hyperbolic paraboloid surface has been one of the most popular mathematical forms for architects. Named Hypar in short, this is the Quadric Surface equation of the Hyperbolic Paraboloid. Erik Demaine summarizes several examples from architecture such as the roof of the Girls’ Grammar School in London (designed by Chamberlin, Powell, and Bonn), the Philips pavilion at the 1958 Brussels exhibition designed by Le Corbusier, and […]

This time, in order to develop a potential “dummy” surface for Grasshopper experiences, I built a better definition. The Graph Surface definition uses a polygon as a basis, divides the edges and moves them according to various parameters. It’s fun to play with mapping different graph types and various polygons and subdivision values. Surprisingly, this definition led me to a wide range of possibilities I haven’t planned. Especially, shifting the graph […]

The smooth and continuous nature of the “Sine Surface” has garnered significant popularity among designers and architects alike. This captivating curved surface offers a visually pleasing aesthetic that adds an elegant touch to various design projects. Its flowing contours and gentle undulations create a sense of harmony and organic beauty. Recently, I delved into this with the help of Grasshopper’s Graph Mapping functionality, I began my artistic journey. Although I […]