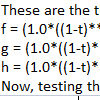Here is the shortest possible way of generating quick parametric curves in Rhino Python. So, you may change the f, g, and h functions to test any function curve. In this Python code, the list comprehension [(f(t), g(t), h(t)) for t in [t0 + i*dt for i in range(int((t1-t0)/dt)+1)]] works by first generating a list of t values from t0 to t1 with an increment of dt using the inner […]

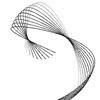
Today’s beautiful curve is the spherical cycloid. It is a cycloid, rolling on a 3d circular path rather than a straight and 2d one. There are algebraic explanations of this curve. Therefore, I find it interesting to experiment with them, since it is more interesting than the regular planar cycloids, epicycloids, and hypocycloids. This curve is believed to have been studied first by Jean Bernoulli in 1732. The interesting and […]

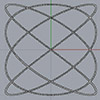
Lissajous curves, named after the French physicist Jules Antoine Lissajous are a family of curves that emerge from the interaction between two harmonic oscillations. They have applications in various fields including physics, engineering, and signal processing. They are commonly used in electronic devices such as oscilloscopes to visualize the phase relationship between two oscillating signals. Similarly, they are also useful in mechanical engineering for analyzing and designing mechanisms that involve […]

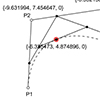
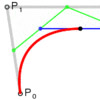
Today’s curve is the beautiful Bezier curve. A series of linear interpolations between the coordinates of control points describe a Bezier curve. So, I created a simple tool in Grasshopper called Bezier Function Extractor to experiment with this elegant construction. In the linear form (degree 1) the linear interpolation between 2 points (P1 and P2). The point at parameter t (0<= t <= 1); Q = tP1 + (1-t)P2. In […]

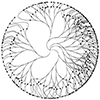
This Grasshopper exercise is a special one. I used Hoopsnake components to develop the branching design I studied earlier here. This time I multiplied the number and orientations of several tree structures to generate my interpretation of the Tree of Life. The challenging part of the algorithm was to finalize every branch tangent to a predefined circle. Group 3 handles this issue by utilizing a Blend Curve component. There are […]

This is the continuation of the previous post on parametric curve equations. In this new version, the script picks a NURBS curve from the user. Then, it analyses the curve’s degree and control points. Unfortunately, only the curves with degree+1 number of control points can be processed. In the future, I hope that I will be able to extend this script to include multi-span curves with more than degree +1 […]

The parametric curve equations are good examples to demonstrate the bridge between computer-aided design and mathematics. Although useless and pointless, it is a good exercise to extract the curve equations. In this Rhino Python code, I present a generalized equation extractor for Rhino. Rhino curves are good examples de Casteljau and Bézier curves. You can see the mathematical underpinnings of Rhino curves with this exercise: This code asks the user […]

This is a new paper published in Nexus Network Journal. I tried to implement euclidean constructions by compass in the approximation of famous parametric curves; Bézier curves, and B-Splines. Then, I created the algorithms to calculate the number of steps on a compass-only construction of Bézier curves. I developed a simple Python script to simulate the geometric constructions. However, I have been studying this topic for nearly four years. In […]

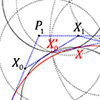
I realized this method of constructing basis splines from given control points while searching for a way to teach students about basis splines. I couldn’t find an easy and visual method to create clamped basis splines by connecting simple cubic Bézier spans. It is a tough job and requires lots of complex equations. However, I suddenly realized that there is a special way of doing that. So I decided to […]

Below is the Python code you can run in Rhino, that draws a cubic Bézier curve (degree 3). As you can see, the Rhino Python code is very slow and inefficient because we calculate every point with lots of computations. Instead, we can use the spline formulae to make this quicker but I wanted to show that the mathematical construction is parallel to the geometric one. This is a nested […]

This RhinoPython script handles the simple graphs of two-dimensional parametric functions. Therefore, it approximates these functions by drawing parametric curves. It generates many points by solving the functions. The graph of parametric functions is a major topic in most Design Mathematics courses. Because it looks like the building block of many concepts of CAD. However, there is much more to learn before saying that the third degree NURBS is a […]

Studied earlier in Grasshopper here, creating a cycloid-like curve actually mimics the physical process of rotating disks on a path. Below is a test in Rhino Python. # Drawing Cycloid-like Curves # 07.08.2017 www.designcoding.net – Tugrul Yazar import rhinoscriptsyntax as rs curv = rs.GetObject(“Select curve”) qual = rs.GetInteger(“Quality”,100) radi = rs.GetReal(“a radius”,4) radi2 = rs.GetReal(“Circle radius”,4) cua = rs.OffsetCurve(curv,[1,1,0],radi2) cevre = 2 * 3.1415 * radi mimi = [] for […]

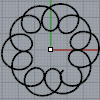
This is a Cycloid-like family of curves, generated by its classical description: a rolling circle. I had several other studies on similar topics before. In this cycloid experiment, I used Grasshopper in which, we don’t need to roll the circle. Instead, we can divide a parametric curve, utilizing data lists to simply rotate a circle around it. Finally, evaluating the circle repeatedly creates a Cycloid-like result. I found this as […]

While testing Anemone components for Grasshopper, I accidentally generated these branches by looping. In fact, I was trying to develop the definition that mimics the well-known “Arch SED” component method. This method uses the tangent vectors for the endpoints of the arcs. Then, it iterates the process in a random fashion so that the branches (arcs) join nicely. Anyway, this definition develops new branches from a previous one. It does […]

Here is the video of the project Life Sciences, designed together with Fulya Akipek, and engineered by Filika Interactive. To be presented in the 2014 Vitra Contemporary Architecture Series Exhibition, Life Sciences is an interactive project produced by Filika Interactive using Openframeworks following the conceptual and visual design by Fulya Özsel Alipek and Tuğrul Yazar. The project is an interactive presentation of the content obtained from the interviews made with primary education […]

Grasshopper still surprises me. This definition draws a spiral by using a random component. It is obvious that the seed value of the random component has a relationship with an archimedean or a similar spiral. My intention was to create a definition to put a number of random points inside a circular area, not a rectangular one. While I grow the radius of a circle and get a t parameter […]

In this exercise, Grasshopper draws various Archimedean spirals. It constructs polar points and maps them onto a range of angles and a number of points. The spiral’s turning speed is determined by the constant “a,” while the constant “n” gives unique names to the spirals by raising the angle variable to the power of 1/n. Wolfram Mathworld names the spiral with n = -2 as lituus, n = -1 as […]

Today, we’ve discussed ways of subdividing entities to create parametric definitions. Curves can be divided into segments, creating snake-like object definitions. This exercise is important regarding the management of data. Vectors and planes are used as reference entities here. Nowadays, it became clear to me that, reference planes are very important because they both include reference points and related vectors as well. The definition studied in this post includes a curve […]