Although it appears simple, Goldberg Polyhedra in Grasshopper became a tough challenge, which I like. I spent about 24 hours attempting to generate these. I started with Goldberg’s original method. This creates an equilateral triangle using coordinates denoted as m and n on a hexagonal grid. Then, we place this triangle onto the faces of an icosahedron. Finally, we project them onto a concentric sphere. We can create many polyhedra […]
Posts categorized under Paneling
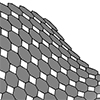
It is not possible to cover a double curvature surface with planar quads. Here is one method that overcomes quad tiling on double curvature by pulling one vertex of the quads to the plane defined by the other three. This method was used in architecture on several occasions such as the exterior facade of The Yas Hotel, designed by Asymptote Architecture in 2009. The same approach is also evident in […]
Here is a simple pavilion design I call the Turtle Pavilion. It was exceptionally easy. The planar shapes placed on the sphere continue to be planar after the ellipsoidal deformations. I was amazed when I first noticed this, for some reason. With Grasshopper’s Facet Dome component, we can panel spheres as we desire. When we deform these panels in the X, Y, and Z directions, they continue to remain planar. […]
As the design of free-form architectural surfaces becomes easier, questioning and foreseeing the feasibility of the construction of these surfaces becomes important. Such an inquiry requires sufficient knowledge of architectural geometry besides the knowledge of materials and structural systems. In this article, we present a preliminary example of a guide. It supports the design and production process of building surfaces with different geometric properties is presented. This guide aims to […]
Back in 2011, one of the first posts on designcoding explored how to divide a surface in alternative ways. I called this Grasshopper definition a semi-regular surface tessellation. Although the term isn’t entirely accurate -since the pattern is neither planar nor made of equilateral shapes- it still reflects what I had in mind. Dividing surfaces into fabricable parts remains a key concept in learning parametric modeling, so I decided to […]