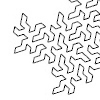
Anemone components are still working great, extending the abilities of Grasshopper. Here, I studied a space-filling (or plane-filling) fractal called the Gosper-Peano Curve. You should be very careful about the number of iterations (the N input). Because it can crash your Rhino if you change it to more significant numbers. Also, you should have Anemone components installed in order to run this definition. The generator curve is a special one. […]

Studied earlier in Grasshopper here, creating a cycloid-like curve actually mimics the physical process of rotating disks on a path. Below is a test in Rhino Python. # Drawing Cycloid-like Curves # 07.08.2017 www.designcoding.net – Tugrul Yazar import rhinoscriptsyntax as rs curv = rs.GetObject(“Select curve”) qual = rs.GetInteger(“Quality”,100) radi = rs.GetReal(“a radius”,4) radi2 = rs.GetReal(“Circle radius”,4) cua = rs.OffsetCurve(curv,[1,1,0],radi2) cevre = 2 * 3.1415 * radi mimi = [] for […]

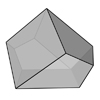
According to Wolfram, “By the duality principle, for every polyhedron, another polyhedron exists in which faces and polyhedron vertices occupy complementary locations. This polyhedron is known as the dual, or reciprocal”. We can use this method to generate new polyhedra from known ones. I tried to develop a Dual Polyhedra Generator in this Rhino Python script. First, the script asks a user to select a closed polysurface object. Then, it […]

We will see a simple Rhino Python exercise here. I called these Polygon Fractals (or Pentaflakes sometimes). It is both educational and fun to play with them. In Rhino, it can be a good exercise for basic CAD commands and transformations such as move, copy, and scale, and precision drawing operations such as object snapping. Also, in Grasshopper, it can be a good challenge for looping. In Rhino Python, it […]

A simple Rhino Python script that generates fractal curves. An example is a test with the Gosper-Peano curve. However the script is not supporting segment directions, which is why the result is not the intended curve. Curve directions could be implemented in the future. # Drawing Simple Fractal Curves # 31.07.2017 www.designcoding.net – Tugrul Yazar import rhinoscriptsyntax as rs import copy initials = rs.GetObject(“Select Initial Shape”,4) referenceA = rs.GetPoint(“Place Reference […]

Studied earlier in Grasshopper here, the sunflower spiral or Phyllotaxis, or Fibonacci’s spiral could be drawn as an exercise of looping in Rhino Python. According to ChatGPT: Phyllotaxis is the arrangement or patterning of leaves, flowers, or other plant parts around a stem or axis. Thus, it refers to the specific geometric arrangement of these structures in plants. The term “phyllotaxis” comes from the Greek words “phyllon” (meaning “leaf”) and […]

This Rhino Python code calculates the cross-product determinant used to determine the orientation of three points (current, next_point, and point) to see if they form a left turn or a right turn. This is a well-known technique in computational geometry to check the relative orientation of points. In this script, the direction is the cross-product determinant that determines the relative orientation of the points. If the result is negative, the […]

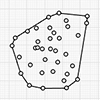
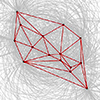
Boris Nikolayevich Delaunay was a Russian mathematician and mountain climber. He developed the Delaunay triangulation, which is a method in computational geometry. It is a triangulation of a set of points such that no point is inside the circumcircle of any triangle formed by the points. It’s widely used in computer graphics and mesh generation. In 2013, I made the brute force code in Rhino Python which is a slow […]

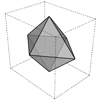
Exercising the “folding” process of a nine-faced solid. Start from its net, and analyze the matching edges. Then, use sphere intersections to calculate the rotation angles. Visit here for more information about this solid: http://aperiodical.com/2013/10/an-enneahedron-for-herschel/

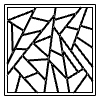
This python code proves how much effort it takes to create a simple hexagonal tessellation. There are, of course, much easier and faster methods than this. But here you see a code that introduces students to Rhino Python. Using this code, a new Rhino command can be generated, and for the first time in Rhino, we can have a command that creates a hexagonal grid. I followed this tutorial to […]

This is a classical method of generating tree-like forms utilizing a simple command “Arc SED”. The idea is simple, as the command draws arcs using an input direction vector, so this could easily be implemented creating a “smooth” composition of curves just by iteration. Actually, this has been a previous study, discussed before here, using Hoopsnake. Now, this time I’m implementing the same algorithm using Anemone and a couple of other […]

Utilizing “Force Field” components of Grasshopper to show my students how it is easy to develop flexible surfaces in design. The classical parametric canopy design is introduced in this video: According to Wikipedia; In vector calculus, a vector field is an assignment of a vector to each point in a subset of space.[1] A vector field in the plane, for instance, can be visualized as a collection of arrows with […]

The A-Chord folding structure was developed and constructed for the World Wood Day 2015 event in İstanbul. The structure had fifty wooden struts of 4 cm X 4cm with changing heights from 200 cm to 230 cm. Two struts joined with a hinge enabled the folding motion of the structure. Thus, the nearby unit is folding in the opposite direction. The Grasshopper model generated all construction details and drawings automatically. As a result, […]

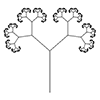
Based on this post, the problem of modeling tree-like fractal shapes is still a good question for the early years of computational design education. Last time, I used Rhino’s macro to study these fractal trees in an “impossibly” limited interface. But this time I used a VB.net script. Here is the code inside of the VB.net component: Here are the inputs. x is the number of iterations. The Crv input is […]

Further studying iteration in Grasshopper, this time, inspired by George Stiny’s “Chinese Ice-Ray Lattice” subdivisions with Aneome, instead of the Hoopsnake add-on I tried in the previous work. As you know, loops add various ways of usage to Grasshopper. In future versions, loops may cease to be just an add-on and become native components of Grasshopper. Until then, loop plugins like Anemone take on this task. In the example here, […]

This is a useful tip both to solve some of the problems with custom surface subdivisions, and to explain the uses of parametric surface evaluations (the U, V, W thing) and the practical use of data lists. Step 1: Put your points inside 0,0,0 and 1,1,0 so that the resulting coordinates can easily be converted to U and Vs. In the example, we are putting some random points between 0,0 and […]

Finally, I had a chance to test and understand the force fields tab in Grasshopper. It creates a continuous vector field inside of a given boundary. Therefore, it is very useful if you want to create an effect of the continuous presence of a force, such as gravity. The Wikipedia definition of a vector field is very basic and understandable: In vector calculus and physics, a vector field is an assignment of a vector to each point […]

This quick project was about a special tiling pattern inside a multi-story residential building’s hallways in Grasshopper. While drawing the construction documents of the project, it was necessary to apply some coding here, as each floor had a different shape to be tiled. Although it is not a real Herringbone tiling, I named it because I couldn’t find a better name yet. First, I’ve imported the geometric boundaries and the “middle curves” […]

Euclidean constructions, when represented computationally, rely on algorithms and mathematical principles to generate geometric shapes and forms. Through precise calculations and logical operations, a computer program can emulate the actions of a compass and straightedge, constructing lines, circles, and polygons with accuracy and efficiency. These digital incarnations of Euclid’s timeless techniques enable the exploration of geometric concepts and the creation of visually captivating representations. This project is interesting because of […]

This is the final Grasshopper sketch of our graduate studio conducted together with Fulya Akipek at Yıldız Technical University Computational Design Unit. The project was about designing parametric “Landscape Extensions” at Kabataş Park. I hope I’ll be able to post the actual student works and the material system, but now; only the final result of the digital sketch we’ve developed together with students is presented here. This was a kind […]