Research

Today’s beautiful curve is the spherical cycloid. It is a cycloid, rolling on a 3d circular path rather than a straight and 2d one. There are algebraic explanations of this curve. Therefore, I find it interesting to experiment with them, since it is more interesting…

Gyroid is a popular triply-periodic minimal surface. Although it is a mathematical entity, designers and architects like its approximations very much. We used an interpretation of Gyroid in the rammed-earth structure: “Common-action Wall” in 2017. In that project, we utilized its spatial quality of dividing…

An Archimedean solid is a convex isogonal (vertex-transitive) and nonprismatic solid that is composed of two or more regular polygonal faces. There are thirteen such solids in geometry. Coding the snub dodecahedron study aims to generate one of these solids, composed of 12 regular pentagons,…

Curvature can be roughly described as how much a curve is “turning” at point a P. We place two “very” close tangents and measure the difference between them. The closer these tangents are, the more precise our approximation would be. An osculating circle is a…

Truncation refers to the process of shortening something by removing parts. You can apply truncation to numbers, text, or data in various contexts. A truncated polyhedron is a geometric solid formed by truncating the vertices of a regular polyhedron. Truncation involves cutting off the corners…

In 1986, Craig Reynolds developed an algorithm aiming to model the flocking behavior of birds, which remains a cult method used in flock simulations today. In my initial study, the bird-oids (boids) have no rules or limitations, just chilling randomly on the screen. I call…

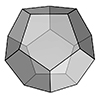
Here is a method for coding the dodecahedron and all its irregular variants in Grasshopper as quickly as possible. I utilized the golden ratio rectangles, usually used to construct the sister polyhedron, the icosahedron. However, the magic component of the Grasshopper, the Faceted Dome rescued…

This is the new version of my previous study on the deformation of Islamic Patterns. I love the purity and simplicity of the geometric construction processes of these patterns. It is possible to observe them in many places in many different forms. By continuing this…

This is the continuation of my previous study on the Fibonacci lattice on a spherical surface, creating a Fibonacci Dome structure. The panelization of curved forms with flat surfaces has been a favorite topic in architectural geometry. The trigonometric layout of the Fibonacci sequence generates a…

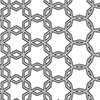
The rhombitrihexagonal tiling is one of the semi-regular tessellations. It is composed of regular hexagons, squares, and triangles. It is a periodic tessellation since you can copy the fundamental unit and move it across the plane to generate the tiling. I use this quality of…

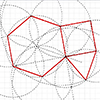
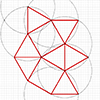
The snub square tiling is one of the semi-regular tessellations, where regular triangles and squares match perfectly to fill the plane without gaps or overlaps. The Euclidean construction of Snub Square tiling is possible by utilizing the basic compass and straightedge operations. I made this…

This work emerged out of necessity. In the design and application process of wooden frame structures, where we put thousands of pieces together like a puzzle, the issue of preparing and updating quantity and measurement lists requires the most effort. Hours spent on this and…

The regular dodecahedron is one of the five Platonic solids, characterized by having 12 regular pentagonal faces, 20 vertices, and 30 edges. When you elongate it, you extend its structure in one or more directions, resulting in a shape that retains the basic properties of…

Today’s computational curve is the beautiful Sierpinski Triangle. It is a fractal named after the Polish mathematician Waclaw Sierpinski, who described it in 1915, though it had been previously described by other mathematicians. It is a self-replicating pattern that arises from a simple recursive process….

This is a 3d modeling tutorial for the platonic solid of dodecahedron. Modeling a dodecahedron is a good exercise for the basic transformation commands such as Rotate3D in Rhinoceros. You will see that it is possible to calculate the rotation angle by using sphere intersections….

The rhombic dodecahedron is a polyhedron with twelve rhombus-shaped faces, where each face has four sides of equal length. It is possible to construct the space-filling variant of the rhombic dodecahedron by arranging multiple such rhombic dodecahedra in a regular pattern so that they fill…

Lissajous curves, named after the French physicist Jules Antoine Lissajous are a family of curves that emerge from the interaction between two harmonic oscillations. They have applications in various fields including physics, engineering, and signal processing. They are commonly used in electronic devices such as…

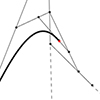
This is a short video tutorial on the B-Spline decomposition I studied earlier here. This tutorial demonstrates how to decompose a B-Spline curve into Bezier curves using Rhino. Despite the original Bezier-de Casteljau algorithm requiring degree+1 control points, Rhino allows drawing a degree-3 curve with…

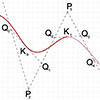
In this short tutorial, I am going to show you how to locate a parametric point on a Bezier curve. This will be a third-degree cubic Bezier curve. So, I start by placing four control points. I name these points from P0 to P3. Then,…

Geodesic refers to the shortest path between two points on a curved surface. It is based on the principles of geodesy, which is the science of measuring the Earth’s shape. On the other hand, in architecture and design, a geodesic dome is a spherical or…