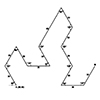
In computer-aided design (CAD), a polyline is a series (or a chain) of straight lines. Each straight section of a polyline is a “segment,” and the points where the segments connect are “vertices.” If a polyline’s starting and ending vertices coincide, it is a “closed polyline” or a “polygon”. If they do not, the polyline is classified as an “open polyline.” Polylines can be planar (2D) or 3D. The Gosper […]
Posts categorized under Research
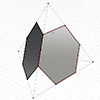
Below is the first paper of my son, Mete Yazar. It is about a mathematical and geometric exercise of calculating the surface area of an arbitrary shape (a classical guitar’s body panel). He did a good job in utilizing Bezier/de Casteljau curves and generating the parametric equations of the piecewise curve. I helped him to validate the results by using rhinoceros CAD software. Therefore, it seems that his calculations are […]
ASCII art is a graphic design technique that uses characters from the ASCII (American Standard Code for Information Interchange) set to create images, symbols, and designs. This form of art involves arranging text characters to form a visual representation of objects, scenes, or abstract patterns. I first encountered this art form in the 90s through readme text files and computer games. Years later, attempting to automate it in Grasshopper was […]
Holger Strøm designed the famous IQlight system in 1973. After more than 50 years, it is still a popular, innovative, and smart design. The IQlight is a self-assembly lamp composed of interlocking quadrilaterals. By utilizing polyhedral geometry, you can generate various shapes and sizes. I created a model of one of the most common IQlight designs, fitting it onto the Catalan solid known as the rhombic triacontahedron. This solid is […]
In architectural research, a significant challenge in robotic fabrication is replicating setups due to the unique configurations used in each study. There is a lack of a unified software platform connecting various researchers and their robotic setups. Additionally, the fabrication tools are typically not open-source and may not be versatile across different scenarios. I suggest using Grasshopper’s parametric modeling capabilities to address these challenges to create flexible robotic tools. Specifically, […]
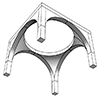
A pendentive is an architectural feature used in domed structures. It is a triangular section of a sphere that allows for the transition from a square or polygonal base to a circular or polygonal dome. Pendentives curve upward from the corners of the base and support the dome above. They help distribute the dome’s weight more evenly and enable the construction of a dome over a non-circular base. I created […]
This is the latest reel video of the Online Virtual Studio (OVS) project. We conducted it together with Oğulcan Üneşi and Serkan Uysal since 2022. We tried to develop a tool for online and blended education in architectural studios. The tool has specific features tailored for design studios. İstanbul Bilgi University Scientific Research Fund partially supported this project. This video showcases the latest toolset OVS provided. The tool takes some […]
Here is the shortest possible way of generating quick parametric curves in Rhino Python. So, you may change the f, g, and h functions to test any function curve. In this Python code, the list comprehension [(f(t), g(t), h(t)) for t in [t0 + i*dt for i in range(int((t1-t0)/dt)+1)]] works by first generating a list of t values from t0 to t1 with an increment of dt using the inner […]
Modeling a rhombicosidodecahedron requires exploding and extending the faces of a dodecahedron and an icosahedron of the same edge length. We begin with both polyhedra centered at the same point. Then, we explode the faces of the dodecahedron and icosahedron outward from the center. We extend their planes while maintaining their orientation and shape. As these faces extend, they intersect and form new polygonal regions. Triangular and pentagonal faces emerge […]
Today’s polyhedra are the famous Archimedean Solids! I created a simple Grasshopper script to generate pendants from these beautiful solids. I call this Archimedean Pendants. However, you can implement other polyhedra to the same code. I hardcoded the vertex coordinates so you won’t need an extra add-on to generate the polyhedra. Thanks to the new SubD component Multipipe, it makes life much easier to produce 3dprint-ready results. To make this […]
Urban Atölye, led by architect Nilüfer Kozikoğlu initiated the development of this Grasshopper code. The concept was to create a random relief pattern on a surface to be carved out using CNC technology. In Turkish, this technique is referred to as “kaşıklama,” as the resulting shapes resemble those carved out by a spoon. Consequently, I named this Grasshopper definition “spooning.” The definition employs the Populate Geometry component to achieve a […]
The Image Sampler has always been a very effective Grasshopper component. Once again, I had the opportunity to use this component for a professional job. As you can see, with the help of a straightforward and short script, we can create a relief of an image to fit the desired panel dimensions on the screen. We can process this onto a suitable material using a CNC mill, laser cutter, or […]
Here is a wave generator code I developed using Grasshopper and Python. While searching for a solution to the realistic water simulations, I came up with the Gerstner Waves. I tried to implement it. However, I came up with this final result, which is not a Gerstner Wave generator, but a much simpler one. It combines many user-fed wave components and calculates the resulting single wave. I played with this […]
A Penrose tiling exemplifies a type of tiling known as aperiodic. In this context, tiling involves covering a plane with non-overlapping polygons or shapes. Aperiodic means the tiling lacks arbitrarily large repeating sections. These tilings derive their name from mathematician and physicist Roger Penrose, who extensively studied them during the 1970s. Despite their absence of translational symmetry, Penrose tilings can exhibit both reflection symmetry and fivefold rotational symmetry. I created […]
It is not possible to cover a double curvature surface with planar quads. Here is one method that overcomes quad tiling on double curvature by pulling one vertex of the quads to the plane defined by the other three. This method was used in architecture on several occasions such as the exterior facade of The Yas Hotel, designed by Asymptote Architecture in 2009. The same approach is also evident in […]
Today’s beautiful curve is the spherical cycloid. It is a cycloid, rolling on a 3d circular path rather than a straight and 2d one. There are algebraic explanations of this curve. Therefore, I find it interesting to experiment with them, since it is more interesting than the regular planar cycloids, epicycloids, and hypocycloids. This curve is believed to have been studied first by Jean Bernoulli in 1732. The interesting and […]
Gyroid is a popular triply-periodic minimal surface. Although it is a mathematical entity, designers and architects like its approximations very much. We used an interpretation of Gyroid in the rammed-earth structure: “Common-action Wall” in 2017. In that project, we utilized its spatial quality of dividing the space into two intertwining and symmetrical volumes. By making one of these volumes solid, I left the other void. So, in this tutorial, I […]
An Archimedean solid is a convex isogonal (vertex-transitive) and nonprismatic solid that is composed of two or more regular polygonal faces. There are thirteen such solids in geometry. Coding the snub dodecahedron study aims to generate one of these solids, composed of 12 regular pentagons, and 80 regular triangles. You can generate the snub dodecahedron by expanding and twisting the faces of a dodecahedron outward. This also creates rhombicosidodecahedron, which […]
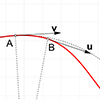
Curvature can be roughly described as how much a curve is “turning” at point a P. We place two “very” close tangents and measure the difference between them. The closer these tangents are, the more precise our approximation would be. An osculating circle is a tangent circle that has the same curvature as the curve at point P. The larger the circle, the more “flat” the curve is. An infinitely […]
Truncation refers to the process of shortening something by removing parts. You can apply truncation to numbers, text, or data in various contexts. A truncated polyhedron is a geometric solid formed by truncating the vertices of a regular polyhedron. Truncation involves cutting off the corners or vertices of the polyhedron in such a way that the original faces become polygons with new edges. This process creates new faces at the […]