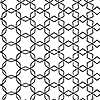
The design of Chinese window lattices named “ice-ray” is one of the classic studies of Shape Grammars. It is an old and good example of algorithmic design. George Stiny explained their geometric construction based on the parametric Shape Grammars approach. He explained shape rules and the abstract machine that produces the subdivisions. I was especially interested in Shape Grammars when I was a graduate student. I even made a prototype […]

This is another starting point for pattern generation study in a dataflow environment. I tried to implement the parquet deformation of Islamic patterns in Grasshopper. I studied Hankin’s method of Islamic Pattern generation. Then I tried to simulate his process beginning with basic regular tiling (regular hexagonal tessellation). Craig S. Kaplan (here) explains this and other methods in his dissertation. A Simple Foundation We have already experienced the result of […]

This study includes three main topics related to the basics of Grasshopper. The first one is the surface subdivision, the parametric definition of a surface component, that is, in this case, a simple pyramidal object. The second thing is the associative behavior of surface components with an external parameter, that is another entity in space; a curve. Traditionally, this is simply demonstrated by 1) finding the area centroids of each […]

A previous work showed a method to create interlocking structures to be created without boolean operations. This time, a small addition is made to create waffle objects using two surfaces, one is the top surface, and the other is the bottom. It was a small modification at the beginning; to replace the “extrude” component with an “edge surface” component. But the interlocking details are now different at each intersection, so […]

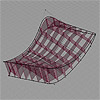
The regular component design technique can be further improved by adding several manipulations. The purpose of this study was to create a surface component that reacts to an inherent parameter (actually a geodesic curve on the surface). However, within the process of parametric modeling, diverse formal potentials emerged. Most interesting results are achieved by adding a graph parameter to control the waves of reaction while splitting the surface as stripes. […]

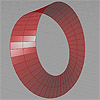
A Moebius strip, also known as a Moebius band, is a fascinating mathematical object and a type of non-orientable surface. It was discovered independently by the German mathematicians August Ferdinand Möbius and Johann Benedict Listing in the 19th century. To visualize a Moebius strip, imagine taking a long, narrow strip of paper and giving it a half twist before connecting its ends to form a loop. The result is a […]

This is a basic formation of component-based design in a dataflow environment. A double-curved surface is subdivided and re-constructed using straight sections. Parametric model of a surface construction by variable components. The main data list of subsurfaces are distributed into four distinct lists, that will be used to construct lines out of double-curved quadrilateral faces. Such definitions could be further advanced by adding a precise fabrication detail. Parametric definition can […]

One of the most popular shapes in topology studies is the one-edge, one-face Moebius strip. Here is a basic definition that generates Moebius-like lofted surfaces. I say Moebius-like because, in Grasshopper, Rhino, or any NURBS surface method, I couldn’t manage to model this shape in its real topological singularity. The tricky part of this Grasshopper definition lies at the end, as I take the first segment of the surface, flip […]

I developed this code 13 years ago while learning the fundamentals of Visual Programming in Grasshopper. I was studying the ways of NURBS curve geometry. The animation shows the construction process of several Bezier Curves. In 2024, I optimized the code and added the thickness. The Flow Earring project showcases the beauty of parametric curves. The Grasshopper definition displays the animated construction process and the variations. The flow of the […]

The cellular canopy is an anonymous tutorial on the history recording capability of Rhino. I’ve been using a “pedagogical” version of this tutorial as an educational tool on the introduction to Grasshopper and Parametric Modeling for architects. The interesting thing with such exercises is they quickly attract students’ attention to the process of designing, in other words, “designing the design process”; is one of the first things we should emphasize […]

There are a couple of experiments in different schools about organizing free-form surfaces (walls here) with a composition of modular elements (bricks). Even though they created robots to make such brick walls, I still couldn’t understand why. Although creating a parametric model that calculates the exact locations of bricks, seems very easy at first sight, there came severe problems to solve in order to achieve a correct layout without using […]

Inspired by Andru Pavlov’s design, I used a curve to accomplish grid tearing. It’s straightforward, and from an educational perspective, this exercise includes several potentials on vector arithmetics and graph manipulation techniques. As a design domain, this definition stresses the use of associative entities in a parametric model. Any primitive or complex entity may evoke different parameters in others. You may download the Grasshopper definition here:[2012_01_06_tear]

This was my first serious Grasshopper study. In 2009, I decided to attend a design contest for a campus entrance. Of course, the jury didn’t know that the design resulted from a parametric model. I have called this Parametric Entrance since then. The starting point of this project was the conception of the “entrance” as a design problem related to the project area as a whole, rather than just a […]

It has been a tough problem for me, for the last two days. A parametric model of an interlocking structure (sometimes also called egg-crate, waffle, or contouring structure) can be created easily in Grasshopper using a Contour component. In addition, you need a couple of list management operations and a boolean (or region) difference event. However, Rhino and Grasshopper are very slow at calculating boolean differences on both solids and […]

Since the mid-20th century, the hyperbolic paraboloid surface has been one of the most popular mathematical forms for architects. Named Hypar in short, this is the Quadric Surface equation of the Hyperbolic Paraboloid. Erik Demaine summarizes several examples from architecture such as the roof of the Girls’ Grammar School in London (designed by Chamberlin, Powell, and Bonn), the Philips pavilion at the 1958 Brussels exhibition designed by Le Corbusier, and […]

An octahedron is a polyhedron and platonic solid with 8 faces of identical equilateral triangles. In this post, I will try to explain the drawing and unrolling process of the octahedron. It has a close relationship with the cube as it’s dual. In order to construct an octahedron, we first have to create a square. The main problem of drawing the square is determining the right angle (perpendicular axis) to […]

[2011_12_25_divide] here is the fundamental of surface subdivision in Grasshopper. In order to design a parametric truss exercise, this is the generally accepted starting point. Get a surface from the file, subdivide it into U and V directions to create point lists, and then manipulate these points to create something interesting. Having a list of points would also present good potential regarding attraction with other entities, such as point or […]

I am learning Grasshopper. In this Circle Crossing definition, I tried to create the above pattern (also described in Sunflower Spiral) as simply as possible, this definition creates not only spirals but is also capable of more tessellations I guess. Maybe a three-dimensional equivalent might be studied in the future. As you can see from the definition, I started with a large circle. Then, I divided it into segments and […]

This time, in order to develop a potential “dummy” surface for Grasshopper experiences, I built a better definition. The Graph Surface definition uses a polygon as a basis, divides the edges and moves them according to various parameters. It’s fun to play with mapping different graph types and various polygons and subdivision values. Surprisingly, this definition led me to a wide range of possibilities I haven’t planned. Especially, shifting the graph […]

The dodecahedron is a Platonic Solid with 12 equilateral pentagonal faces. It has a close relationship with its 20-sided dual, Icosahedron. Mete Tüneri showed the following method of Dodecahedron construction, using only distances, corners of the pentagon, and a visionary equilateral triangle underneath. We’ll construct Dodecahedron, assuming that we’ve drawn an initial equilateral pentagon. We need to find out the pentagon’s angle of 3d rotation. First, put spheres at points a […]