Experimenting with various plug-ins for solar calculations, I found Daniel Da Rocha’s robust implementation of the solar position algorithm in vb.net. It calculates the solar angle of any place and time. Although it’s written in the old vb.net component, it still works great. I’m trying to create a fast and easy workflow to optimize Grasshopper models based on solar directions. This is done by projecting faces to the solar planes […]
Posts categorized under Research
This is the continuation of my scripting experiment within Grasshopper. Like the minimum spanning tree algorithm, this is also a famous problem of computational geometry; the shortest path problem. I’m now coding faster and understanding the namespace more easily in Grasshopper. This time, the challenge was implementing Dijkstra’s algorithm for the Shortest Path Generator. Again, it’s a quite powerful algorithm, I even plan to use it in my current project. Although […]
This is the basic form of a surface division, based on curvature. As each point on the surface has a curvature value, this might be used to dispatch those values and see the points at flat and curved parts of the surface. Here is the Grasshopper definition [GHX: 0.8.0066] (Please use right click + save target as to download ghx definitions in this site. Otherwise your browser may try to execute them […]
This is the updated version of my MST code from 2012. After over a hundred hours of Rhinocommon and Grasshopper SDK studies, and lots of dead ends, I was finally able to calculate the minimum spanning tree of any given curve network in Grasshopper. Problems like these are interesting to me because of their clear logic and diverse areas of applications in design. I tried to simulate Dijkstra’s, Kruskal’s, and […]
Trying to further improve my experience in parametric modeling, I’m mixing and joining old definitions to reveal different potentials. I’m experiencing spatial mapping or morphing in Grasshopper. This is an equivalent form of the “flow along surface” command in Rhinoceros. It re-builds a geometric composition over another space (from world XY coordinates onto a surface with UV coordinates here) This is especially useful in creating surface compositions from famous tessellations […]
Another famous shape of architectural geometry is a set of definitions creating minimal surfaces. I’ve found the trigonometric equation of the Gyroid and created a simple logic for approximating it as points in Grasshopper. However, when I searched the net for similar solutions, I found lots of them including the same approach as mine (Wynstan Wu’s definition). I was planning to develop a script in Grasshopper to take these estimated […]
As far as I understood, it is impossible to physically construct double-curved surfaces from quadrilateral and planar faces. This definition tries to find an optimized alternative to this problem. Any surface, single or double curved, is divided into standard sub surfaces. But this time, those surfaces are treated as planar surfaces, therefore one corner is moved to meet this requirement. The output consists of only planar surfaces ready for fabrication. […]
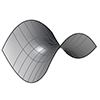
This is another popular “math surface” being rediscovered by designers nowadays, in 2012. Saddle surfaces, seen above as mentioned earlier (here) have a special type named “Monkey Saddle Surface”. This surface was a dramatic example of how Grasshopper can control equations and instantly show graphical results. The mathematical equations start with Z=… this makes it very easy for us to transform any x-y grid centers (a 2d data tree of […]
QuickShaper (QS) an experimental computer utility for Shape Grammars. It aims to assist designers and students in creating and exploring rule-based designs. QS is first presented and published with Birgül Çolakoğlu at the 25th eCAADe Conference held at Frankfurt / Germany in September 29th, 2007. QS is a scripted utility, written in MaxScript, developed within Autodesk’s 3D Studio MAX version 9. It is not tested on earlier versions. QS works […]
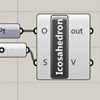
I tried different approaches to drawing platonic solids using Grasshopper’s native components. However, it seems impossible now. In geometric definition, a platonic solid is a set of points, distributed on a sphere with equal distances. If the set contains 12 points, then it’s an icosahedron. I found lots of information about these objects and mathematicians seem to love analyzing them. They created different approaches to building an icosahedron. One of […]
This is another old-school approach to parametric modeling, today known better as part of Building Information Modeling. I tried to create parametric objects in order to understand and learn the capabilities of Revit. That was very useful for me in learning this interface. I specially chose Le Corbusier’s chair set as my first experiment on family creation in Revit. On his 100th anniversary of Eastern Voyage, Le Corbusier’s soul returned […]
After Puzzling, I tried to establish more of Escher’s basic grid transformations using Grasshopper’s native components. This definition simulates Escher’s transformation of four-cornered grids. The postulate is based on the fact that every quadrilateral (or triangular) planar shape can create regular tessellations without gaps or overlaps. In the traditional method, this tessellation is achieved by rotating the shape 180 degrees and copying afterward. However, in Grasshopper we simply define the […]
Nowadays, I found myself back into traditional hand sketching. Several failed attempts on Grasshopper led me back there. NURBS (and Grasshopper) somehow limits our conception of surfaces to four-cornered (or two-directional) manifolds. Although it sounds like limiting our designs, having four-cornered component spaces has still lots of experimental fields for designers. Escher is a cult person, who transforms the euclidean coordinate system to meet his design intentions. There are lots […]
This topic of trees and recursive computing is inspired by the method shown here at the Rhino Python 101 Primer. This is a beautiful method of recursion that creates tree-like shapes, composed of arcs. I constructed these arcs by using the Arc SED (start, end, direction) method. This requires start and end points and a vector that is tangent to the arc (at the start point). Therefore, the overall look […]
Today, we’ve discussed ways of subdividing entities to create parametric definitions. Curves can be divided into segments, creating snake-like object definitions. This exercise is important regarding the management of data. Vectors and planes are used as reference entities here. Nowadays, it became clear to me that, reference planes are very important because they both include reference points and related vectors as well. The definition studied in this post includes a curve […]
This was an interesting topic in design computing class. Geometric constructions based on strict relationships are becoming exciting in parametric modeling environments. I think muqarnas includes such a relationship. There is a primary method of modeling this shape, introduced by Mete Tüneri. His solution to a simple parametric muqarnas object includes a surface with six reference points, with two boolean differences (one cylinder and one box) creating the component. In […]
This is the basic definition of one point attractor on a grid of points. [GHX: 0.8.0066] Here, the fundamentals of data tree matching can be studied. A hexagonal grid is exploded into points and new polygons are created there. Instead of a standard point distance relation to polygon size, this time the distance factor affects the rotational angle of these polygons. Although the structure of data trees is getting complicated, this has no […]
That was about six months ago, our study for a design competition required a spatial allocation algorithm. An office building with a rectangular plot and a strict functional requirement forced me to the good old Voronoi diagrams, subdividing a surface. Here is the definition file: [GHX: 0.8.0066]. However, there were other design parameters such as the sunlight and orientations of each functional cell. Combining a couple of graph components helped me […]
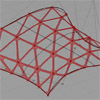
This is the old-method Parametric Truss definition. Interestingly this quickly became a solid solution, used and taught for years. I couldn’t find a better answer yet. As Grasshopper updates, some of the components in this definition change but the overall structure remains. Subdivision of a free-form surface and addition of geometric components has, of course, a wide range of alternatives. Maybe we should combine this with different problems and solutions […]
In this experiment, I’m trying to use data recorder to change components on a surface. The component part is a standart triangular construction, but the attractor points are defined by a 2D slider that is connected to a data recorder. Data recorder remembers last 15 points, while you move the 2d slider, last 15 points are projected on the base surface. This creates an illusion as if a “snake” game […]