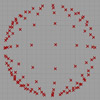
Today’s fractal is the famous Mandelbrot Set. The Mandelbrot set is a well-known and complex mathematical set often associated with fractals and chaos theory. Named after the mathematician Benoît B. Mandelbrot, it’s a set of complex numbers defined by a simple iterative process. The Mandelbrot set is an intricate and self-similar boundary, which reveals increasingly complex patterns at different magnifications. On the other hand, I heard the term “The fingerprint […]

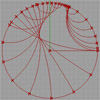
Today’s fractal is the Julia Set, the amazing simplicity of chaos. There are lots of applets and articles on the internet about this fractal. You can generate this with the iteration of a basic function many times and placing points on the complex plane. I developed a Grasshopper implementation in 2012. Also, this was my first study on complex numbers. At each iteration, the detail level increases. I utilized a […]

After a couple of days of studying the mysterious Doyle spiral, I’ve decided to test an approach of circle packing from conformal mapping. First, I tried to understand the Poincare disk (earlier at here, here, and here and here). I used it as the hyperbolic representation of space on a two-dimensional plane. Then, I linked a regular hexagonal grid and rebuilt it after the hyperbolic distortion. This led me to find […]

We can create tessellations of outer points in a Poincare Disk, using the manual method explained in the last post (here). But repeating that compass and straightedge process is becoming a little useless after a couple of repeats. If you say “ok. I understood the concept, let’s get faster!” then we can model just the same process in Grasshopper3D to examine varying results in seconds; If we connect any grid of […]

The poincare disk is still an interesting representation of hyperbolic space for me, full of mysteries. I’ve had several attempts to understand it previously (here and here). Finally, I found a resource* explaining basic concepts about it. I tried to repeat some of the constructions in Rhinoceros, (without any logical purpose). The most important part is the conversion of a Euclidean point into a hyperbolic space. There is no clear […]

This was before Spherical Fantasies, while I was trying to update my surface equation definition. In between designerly intentions and mathematical facts, it’s hard to maintain a process, while keeping the definition yet simple and open to exploration. Grasshopper definition is here: [GHX: 0.8.0066] A little tired of mathematical definitions, I started to give names to the animate surfaces I develop. Like the Spherical one, this is also a trigonometric equation […]

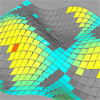
This is about conforming distortions on surfaces and creating imperfect (say ugly) surfaces. I started with planar surfaces, however, I continued with spherical ones. There are interesting results when applying trigonometric functions to spherical surfaces. Example surface equations: W=(sin(x*y)) / 2 and W=(cos(x)+sin(x-y²)) / 2 Please be patient if animations are loading slowly. But they represent a way of creating free-form-looking surfaces, highly mathematical behind the scene. Here is the […]

The Truncated Icosahedron (5,6,6) is an Archimedean Solid we often recognize as the iconic soccer ball. This geometric structure, also affectionately known as the “Buckyball” in honor of the visionary architect Buckminster Fuller, has gained significant popularity and recognition both within the realms of mathematics and everyday life. It is composed of twelve regular pentagons and twenty regular hexagons, meticulously arranged to achieve a harmonious balance. This symmetrical nature makes […]

Truncated hexagonal tessellation (or named 3-12-12) is represented in hyperbolic space (as far as I understood it). The idea is simple if you don’t mix it with complex equations. Below is the 2-dimensional representation of hyperbolic projection. Paper space is defined by the thick line there. Projection is based on a two-sheet hyperboloid surface. Euclidean version of this tessellation is described here. Here is the Grasshopper3D file containing the above […]

[GHX: 0.8.0066] This is my second attempt on getting into non-euclidean representations of space. Althouth it seems easy at first sight, this represents a close point of theory between mathematics and contemporary computational design geometry. As always, architects tend to use mathematical terms such as “non-euclidean geometries” but as far as I saw, most of them have no idea about what it is. So, I’m trying to learn and understand this […]

This is my first attempt at representing a non-euclidean space. There are several representations of a non-euclidean space in euclidean means such as Beltrami-Klein or Klein, Poincare, Poincare half-plane, and Weierstrass. Here, I tried to understand Poincare’s approach. Random straight lines are drawn on a hypothetical hyperbolic space using a simulation of Poincare’s famous disk representation. Although there is a precise description of the disk and its construction, I used a ready-made […]

Using SPM Vector Components developed by two talented people, Daniel Hambleton and Chris Walsh (website here), I’ve studied ways of displaying dynamic diagrams of form. I’ve modified an example file and found myself in a surprising formal exploration. It’s like watching the clouds, giving them meaning like a sheep, a flower, a baby… Here is a link to the Grasshopper file. Right-click and save it to your computer (don’t left-click it) [GHX: 0.8.0066: SPM […]

I’ve worked a little more about the Solar Position definition I’ve started here. The definition uses Danel da Rocha’s beautiful solar position script and utilizes it with other components. It creates visual output for any given surface, divided into quads (with side faces of course) and coloring according to their orientation to the sun. This time (file here: [GHX: 0.8.0066]) I added an occlusion part to calculate the surface’s own shadow. Now, […]

I have come across several high school topics I was afraid of. While I was searching for a geodesic dome definition in Grasshopper, it was quite surprising that I found an easier way of modeling an approximation of icosahedron, the famous platonic solid. Icosahedron was a research topic of this website at various posts before (here, here, and here). In order to generate geodesic spheres, first I had to solve […]

Yesterday, Kağan asked me about the isovist component in Grasshopper and how it works. In fact, it is a long story, I said because once upon a time, I was curious about Space Syntax theory as my old friend Ela Çil introduced it. So, here is an original definition of Michael Benedikt; “The environment is defined as a collection of visible actual surfaces in space. An isovist is the set […]

Creating and handling new types of grid configurations might be an important topic, as Grasshopper is not supporting them natively (yet). I tried to create some semi-regular tessellations based on regular grids. It is actually truncated versions of regular grids, but it slowly becomes interesting as I realized that I may further truncate emerging grids to create Level 2 and Level 3 grids with more complex tessellations. Here are two […]

Not all of them, but when you get the idea, you’ll see there are lots of different alternatives for creating Fuller’s famous Geodesic Domes (Although in fact, he is not the inventor of it). I was playing with Platonic Solids in Rhino and realized that the “Pull” command is very useful in subdividing objects. I modeled this in Rhino 4. First, take a regular Icosahedron and divide it. Because, this […]

Playing with the 2D Metaball component in Grasshopper. I was curious about why there are no Metaballs in 3D in Grasshopper. Then, I realized that in fact, the 2D Metaball component is creating a section of a 3D Metaball computation. I think it is a topic worth studying even 10 years after this original post to develop an easy way to create the metaball surfaces. In 2012, thanks to the […]

Galapagos was a great improvement when it became available natively within Grasshopper as an Evolutionary Solver. However, I couldn’t find time to examine it until recently. This examination gave me an idea of algorithmic thinking, tool making, and tool using. The first experiment shown below tries to solve equilateral triangulation, based on the Delaunay method. Galapagos has two different solvers, named “simulated annealing solver” and “evolutionary solver” shown respectively below. […]

The tetrahedron is a popular platonic solid for designers. We’ve explained how to draw them using equilateral triangles here before. Recently I’ve found (sorry, lost the web address) a much quicker way of modeling a Tetrahedron using a cube. It’s very simple, just connecting the three opposite corners of the cube automatically makes them equal, resulting in the four equal faces. Of course this time you’ll have to calculate the […]