I finally installed Firefly, it immediately powers Grasshopper up with beautifully smart components, even if you don’t have Arduino it is still very useful. If you want to give it a try, first you have to install a small tool free from www.reactivision.com in order to send data to Firefly. After that, you may download and install firefly from their website, www.fireflyexperiments.com. It was the real-time inputs, my first interest. […]

Is it possible to model a two-way parquet deformation using only native components of Grasshopper? In this definition, I limited myself to 10 of them. Parquet deformations are a very interesting and pedagogical topic to teach some of the basics of contemporary parametric modeling. This post explains a minimal parquet deformations algorithm in Grasshopper. However, this has its own limitations. You will see that the definition generates the attractor graph […]

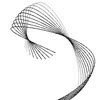
Previous studies on trigonometric surface equations showed me an interesting alternative. This is the modification of the breaststroke surface definition. This time, I’m trying to fix the equation and change input values in a fashion that the waves of the surface are not symmetrical. Here are a few experiments on it; (Size, 44.8, X=10, Y=5, animating X’s from 0 to 32) (Size: 42, X=7, Y=5, animating X’s from 0 to […]

In Turkish, there is a strange word “baklava” that has many uses. According to Wikipedia: Baklava is a rich, sweet pastry made of layers of filo pastry filled with chopped nuts and sweetened with syrup or honey. It is characteristic of the cuisines of the former Ottoman Empire and those of Central and Southwest Asia. However, we should add that 150 gr. of baklava is 413 calories. Here is it […]

It all started with my new passion for origami tessellations, not much of origami, but the tessellation part. I was too lazy to fold it physically, nor model them using an engine such as Kangaroo. That would also be very unnecessary (and yes, very boring) to simulate a folding effort on the computer unless we lose our connection with the real world. Instead, I tried to look at a much […]

You might recall this type of parametric brickwork from architectural classics, such as the Programmed Wall by ETH Zurich and Gramazio Kohler Research, or the facade of the Mulberry House by SHoP Architects. Initially, I explored the simplest method for placing boxes on a surface, but this approach didn’t yield the correct layout. To improve it, I introduced gaps, which not only liberated the wall’s design but also opened up […]

After playing with vector fields in 2d (here) it was quite easy to create a 3d surface deformation. Here is my first experiment on a regular triangular grid’s three-dimensional behavior within a vector space, that includes a point charge of varying z coordinates. That makes field lines escape to a bounding box, instead of a bounding rectangle. Again, you may play with force decay, the number of samples, and the […]

Back to the basics. I finally had time to test the vector fields components in Grasshopper. It was a couple of updates ago, a new tool group emerged in the vector tab, introducing different types of vector fields to users. Then, these fields could be merged to form more complex effects. However, I created a very simple example of how we can use those components to distort a system (such […]

In this exercise, Grasshopper draws various Archimedean spirals. It constructs polar points and maps them onto a range of angles and a number of points. The spiral’s turning speed is determined by the constant “a,” while the constant “n” gives unique names to the spirals by raising the angle variable to the power of 1/n. Wolfram Mathworld names the spiral with n = -2 as lituus, n = -1 as […]

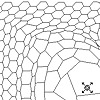
Can we go back to the beginnings of algorithmic design tools, when it was still as simple as possible (not to the binary level of course)? Most of the theorists agree about the fact that contemporary parametric design tools sometimes provide needlessly many possibilities that suppress the designer’s own creativity. The Voronoi component in Grasshopper was one of the cult examples of that (mentioned here). Throughout this blog, I always […]

I’ve been searching for a method to study the Voronoi subdivision in order to manipulate it. There are well-known algorithms for that. But I thought it would be better if I use a projective approach just as I did in studying hyperbolic space (here). This is the metaphor of inflating balloons. However, I inflated cones instead of spheres. This way, it became possible to modify the algorithm. So I was […]

Today’s Architectural Geometry course was about platonic solids and different attractor objects in introducing component-based design systems. Benay’s idea was both pedagogical and interesting to test in Grasshopper. I searched for the most fundamental type of attractor solid in creating a composition such as this; There is a subdivided sphere and an attractor sphere. The pull component works great here. You may use multiple attractor solids or different shapes such […]

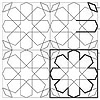
In this exercise, we asked students to develop a method to produce custom tessellations. This is based on the analysis of what is called “Islamic patterns”. We have discussed Eric Brough‘s famous book “Islamic Geometric Patterns”, regarding geometric relationships and linear connectivities via underlying tessellations (such as regular square and hexagonal). Thus, this geometry and drawing exercise is called “Seamless Patterns” in the Design Geometry course at İstanbul Bilgi University. […]

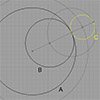
The first-year Architectural Geometry course includes Euclidean constructions as a study of associative geometry. We have exercised the below questions to study this topic. These are three mutually tangent circles, that can be drawn using only a compass and ruler, without built-in tangency functions in Rhino. Such exercises are expected to improve students’ reasoning. We believe architectural geometry education should encourage a conception that allows students to think about what […]

Last week, the first-year architectural geometry course was about pattern deformations. Students are expected to familiarize themselves with 2d drawing, transformation, and control point editing commands while trying to design a deformation. After studying regular and semi-regular tessellations of the plane, they are expected to develop reasoning on the rule-based and iterative processes. This also constructed an underpinning for Basic Design‘s “Metamorphosis” study, where they have discussed more conceptual frameworks […]

The Möbius strip is a famous mathematical object. Although being in three-dimensional space, it is a closed-loop of only one surface and only one edge. This quality alone makes the object an interesting study for computational design. I aimed to create an object to test our new CNC machine. I wanted to test the egg-crate interlocking fabrication method. This is why the study became a Möbius strip fabrication. Apart from […]

This is not to explain the method of the Parquet Deformation but to see the potential. After we’ve studied regular, semi-regular, dual, and truncated tessellations with students, the Architectural Geometry course expects them to develop a Parquet Deformation handmade such as those shown below. I call them Parquet Deformation handmade. Because they are manually designed but drawn using traditional CAD. The samples you see below are from this website. It […]

This is a late update for my 2012 study on Cairo Pentagonal Tiling (or Cairo Tessellation). Originally, it was an exercise of dual tessellations. Because this tiling is the dual of the famous semi-regular tessellation of Snub Square. After coding the Snub Square tiling, I attempted to generate the dual of it. However, that created an inefficient result. This latest version generates the original Snub Square and Cario Pentagonal Tilings. […]

Here is the step-by-step generation of the old Snub Square Tiling. Frankly, this is the first step in the generation of Cairo Pentagonal Tiling I generated with Grasshopper earlier. Because Cairo pentagonal is the dual of a snub square. The first step was easy. Just dispatch cells of a square grid, then evaluate them according to the ratio of 0.366 approx. which is derived from the bisector of an equilateral […]

The intricate harmony of the Islamic Patterns is amazing. The geometry of this and other Islamic pattern designs are explained in the 3rd chapter of Craig S. Kaplan’s Ph.D. dissertation. I constructed a semi-regular tessellation, particularly the 4.8 because it seems to open interesting explorations that mostly emerge from truncated squares. We know equilateral triangles and hexagons are also fundamental shapes for this task. However, the dual nature of the […]