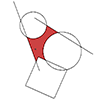
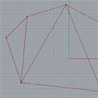
I learned this method from the open math resources website. I couldn’t help myself repeat it in Rhinoceros. It was quite fun to solve circle tangency problems in 2D, this is one of them: drawing the circle that passes three given points, not using ready-made commands but only geometric tools of the circle (compass) and ruler (line). Here is the sequence of it: First of all, we need to know […]
Posts categorized under Research
Here is a simple explanation of the famous Euclidean Constructions: Why didn’t Euclid just measure things with a ruler and calculate lengths? For example, one of the basic constructions is bisecting a line (dividing it into two equal parts). Why not just measure it with a ruler and divide by two?One theory is the the Greeks could not easily do arithmetic. They had only whole numbers, no zero, and no […]
Grasshopper still surprises me. This definition draws a spiral by using a random component. It is obvious that the seed value of the random component has a relationship with an archimedean or a similar spiral. My intention was to create a definition to put a number of random points inside a circular area, not a rectangular one. While I grow the radius of a circle and get a t parameter […]
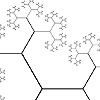
I at the Center is a multiple-axes vertex deformation based on a quadrangular hyperframe, designed by David Oleson at the studio of William Huff in 1964. Below, you see the original drawing and my Grasshopper animation based on a single-point attractor, creating the “I” wherever it is. It was a pleasure to read and repeat this deformation, which is a nice exercise in data tree operations and also one of the […]
Instead of searching for an iterated and rule-based variety, this method captures instances of spatial deformation by transforming the hyperframe. This liberates us from a classical understanding of pattern deformations that are enframed within regular polygons, mostly rectangles or hexagons. Grasshopper has a built-in component to study such variety. The spatial Deform component gets vectors as inputs and transforms any given geometric object according to it. This website has also […]
This was my first parametric patterning study we conducted together with Birgül Çolakoğlu at Yıldız Technical University in 2008. It was based on the pattern exercises we’ve experienced with BOT Graduate Students as a preliminary study within a Computational Design Studio. Later, the CNC fabrications were exhibited at İstanbul Bilgi University Digital Design Symposium. The exercise was about analyzing and reconstructing regular İslamic Patterns via MaxScript. After fundamental instructions about the […]
This is a simple trick that shows the utilization of the “surface split” component in Grasshopper. It is used for detecting the inner regions of any given two-dimensional linework. Thus, it resembles the hatch boundary detection of AutoCAD and similar software. There is no built-in hatch component in Grasshopper. But maybe you can use this as a starting point if you want to develop it. The definition starts with drawing […]
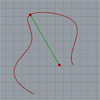
Today’s tip is about two-dimensional curve-point calculations. It is very handy to use “closest point” components in Grasshopper. You can calculate distances and directions between curves, surfaces, and points. Then, place point objects in relation to the proximity of another object. However, there is no “farthest point” implemented yet. I tried to calculate the farthest point from a curve. First, I tried to translate the curve in a fashion that […]
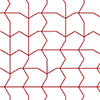
It has been a while since I didn’t post any patterns. Here is a beautiful one from the iconic design studio of William Huff. Crossover Parquet Deformation is a single-axis, line-based deformation algorithm, constructed on a regular quadrangular hyperframe, designed by Richard Lane at the Basic Design studio of William Huff in 1963. It presents two different parquet deformation sequences linked together. Thus, the designer created a transition between the […]
Recently, I returned to old fashion RhinoScripts in order to recapture its idea and functionalities again. After almost 10 years, this is my first experiment on creating a custom function that draws hexagonal grids. I tried to implement a fast process for it, however, there could be much faster ones. This script focuses on using functions, variables, and object arrays. I’ll continue to make more of these simple exercises and […]
After becoming a ready-made component in Grasshopper, the Delaunay triangulation lost its popularity quickly. It used to be a nice problem of computational geometry for designers obsessed with scripting. Last month, Benay reminded me of the method of circle checking. She showed her Rhinoscript that creates circles from point triplets and checks if a point is inside or not. Today I studied this in Grasshopper to see if I can […]
Kündekâri is an old woodworking technique, composed of interlocking parts without any glue or nail. It is primarily used in wooden doors and minbers inside Mosques. The interlocking system makes the whole structure very durable. I tried to model this technique using the Voronoi pattern, naming it Voronoi Kündekâri. Below you see a typical example of Kündekâri pieces and the resulting pattern. The interesting part of the Grasshopper model is […]
This is based on my failure of creating an optimum solution for planar polygonal subdivisions. There is a method called Tangent Plane Intersection (TPI), explained briefly here (sometimes similar algorithms are called “planar remeshing” and “variational shape approximation”) which is effectively used in the Trada pavilion (here). I tried to implement a similar method using only native Grasshopper components and no recursion, but it quickly became much more complicated than […]
Below is a classical Truchet Patterns example we used to discuss in design computing class. Now, we can create a much faster and cleaner definition using the newly added Array component. The new version of Grasshopper brings several important features: Patch surfaces and date/time components. We used to implement a VB component to create simple clocks that measure temporal operations in Grasshopper. Parsing and executing MusicXML and related applications were […]
The story of Atatürk Cultural Center (in Turkish: Atatürk Kültür Merkezi – AKM) dates back to the 1930s. Auguste Perret designed the first version of the project and started the construction in the late ’30s. However, war and financial problems halted the construction. The project continued in the early 1950s with major updates and extensions. Faruk Akçer and Rüknettin Güney were responsible for this second version. Hayati Tabanlıoğlu designed the […]
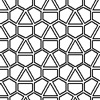
Becoming popular after the Beijing 2008 Olympics National Aquatics Centre‘s facade (which is believed to be a Voronoi subdivision, as an epic mistake), the Weaire Phelan structure is a solution of equal volumes with minimal surface area. Although it is a structural solution, I think for architects, catching the eye with “cute bubbles” seems to be the primary purpose of this structure. (images from arup.com) A More Formal Explanation This […]
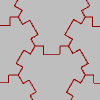
The Parquet Deformation exercise is generally originated with William Huff. Huff conducted it at several schools of architecture since the 1960s. Huff defines the exercise as rooted in two analytical disciplines; monohedral tilings in geometry, and the continuous deformations in biological morphology. This is generally exemplified by D’Arcy Thompson’s and Albrecht Dürer’s studies. One of the student’s works of Huff, Trifoliolate is a single-axis, single-prototile hexagonal parquet deformation. It was […]
I’ve seen beautiful examples of similar compositions made using vector field components in Grasshopper. I just tried to make my own animate field lines to see how they float over force dynamics. In essence, these compositions could also be done using regular vector components but the field components make life much easier by merging different forces together rather quickly. Here is my Grasshopper definition (be careful it may slow the […]
Today’s design computing class was about fractals. In Rhino, writing macro statements are very easy to learn as it just mimics your behaviors in a sequential text. There are a few syntactic rules that we should know. First, you should watch the command line carefully to understand the steps of your design process. Each command in Rhino requires different inputs from the user. In macro, you may enter these values […]
One of the cult texts in Shape Grammars theory is Stiny‘s Chinese Ice-ray Lattices Grammars. Although it is full of technical terms, it represents an analysis of a working algorithm. We can directly transfer that from the behavior of an artist. “One can imagine a Chinese artisan, summoned to a building site. He brings tools and implements and a collection of finely finished sticks. Then, he begins his design by […]