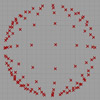
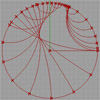
After a couple of days of studying the mysterious Doyle spiral, I’ve decided to test an approach of circle packing from conformal mapping. First, I tried to understand the Poincare disk (earlier at here, here, and here and here). I used it as the hyperbolic representation of space on a two-dimensional plane. Then, I linked a regular hexagonal grid and rebuilt it after the hyperbolic distortion. This led me to find […]

We can create tessellations of outer points in a Poincare Disk, using the manual method explained in the last post (here). But repeating that compass and straightedge process is becoming a little useless after a couple of repeats. If you say “ok. I understood the concept, let’s get faster!” then we can model just the same process in Grasshopper3D to examine varying results in seconds; If we connect any grid of […]

The poincare disk is still an interesting representation of hyperbolic space for me, full of mysteries. I’ve had several attempts to understand it previously (here and here). Finally, I found a resource* explaining basic concepts about it. I tried to repeat some of the constructions in Rhinoceros, (without any logical purpose). The most important part is the conversion of a Euclidean point into a hyperbolic space. There is no clear […]

Truncated hexagonal tessellation (or named 3-12-12) is represented in hyperbolic space (as far as I understood it). The idea is simple if you don’t mix it with complex equations. Below is the 2-dimensional representation of hyperbolic projection. Paper space is defined by the thick line there. Projection is based on a two-sheet hyperboloid surface. Euclidean version of this tessellation is described here. Here is the Grasshopper3D file containing the above […]

[GHX: 0.8.0066] This is my second attempt on getting into non-euclidean representations of space. Althouth it seems easy at first sight, this represents a close point of theory between mathematics and contemporary computational design geometry. As always, architects tend to use mathematical terms such as “non-euclidean geometries” but as far as I saw, most of them have no idea about what it is. So, I’m trying to learn and understand this […]

This is my first attempt at representing a non-euclidean space. There are several representations of a non-euclidean space in euclidean means such as Beltrami-Klein or Klein, Poincare, Poincare half-plane, and Weierstrass. Here, I tried to understand Poincare’s approach. Random straight lines are drawn on a hypothetical hyperbolic space using a simulation of Poincare’s famous disk representation. Although there is a precise description of the disk and its construction, I used a ready-made […]