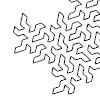
The Hilbert Curve is one of the results of David Hilbert’s vision of mathematics as a network of symbolic systems. Defined in 1891, this curve is a fractal that fills a two-dimensional plane with a one-dimensional line in the limit. It exhibits self-similarity. It emerged from representing higher-dimensional spaces through continuous, lower-dimensional entities. A curve that grows within a bounded area remains continuous but non-differentiable. Yet it possesses infinite length. […]

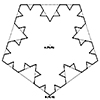
The Koch pentagon is a fractal shape that starts with a regular pentagon. Here, we divide each side of the pentagon into three equal parts. Then, we replace the middle with two sides of an outward-pointing equilateral triangle. We repeat this process for every new side in each iteration, creating a self-similar pattern. Helge von Koch (1870–1924) was a Swedish mathematician known for his analysis and number theory work. He […]

A fractal is a complex geometric shape that we can split into parts, each of which is a reduced-scale copy of the whole. This property is self-similarity. Fractals often exhibit patterns that repeat at different scales. We can find fractals in nature, such as in snowflakes, mountain ranges, trees, and clouds. We can also generate them mathematically. Fractals have applications in various fields such as physics, biology, and computer graphics. […]

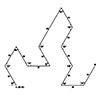
The Flowsnake, or Gosper curve is a space-filling fractal. It is also known as the Peano-Gosper curve. There are other similar space-filling fractals such as the Dragon curve, or the Hilbert curve. A space-filling fractal is a special type of curve, that fills a plane when iterated infinitely. This means, that if you continue to replace every segment of the polyline with the whole drawing, it will quickly become very […]

In computer-aided design (CAD), a polyline is a series (or a chain) of straight lines. Each straight section of a polyline is a “segment,” and the points where the segments connect are “vertices.” If a polyline’s starting and ending vertices coincide, it is a “closed polyline” or a “polygon”. If they do not, the polyline is classified as an “open polyline.” Polylines can be planar (2D) or 3D. The Gosper […]

Today’s computational curve is the beautiful Sierpinski Triangle. It is a fractal named after the Polish mathematician Waclaw Sierpinski, who described it in 1915, though it had been previously described by other mathematicians. It is a self-replicating pattern that arises from a simple recursive process. To construct the fractal, you start with an equilateral triangle and then repeatedly remove smaller equilateral triangles from its interior, leaving holes. Each iteration involves […]

The Hilbert Curve, also referred to as the Hilbert space-filling curve, was initially introduced by the German mathematician David Hilbert in 1891. It is a continuous fractal curve, presenting a variation of the space-filling Peano curves uncovered by Giuseppe Peano in 1890. After a study on the mathematical background of this curve, I implemented a Python code into Grasshopper Python. However, I wanted to explore more variations by playing with […]

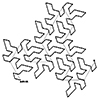
This week’s fractal is the famous Dragon Curve. Dragon Curve exhibits self-similarity, meaning parts of the curve resemble the overall shape, regardless of scale. It’s fascinating because a relatively simple construction process generates a complex and visually captivating fractal pattern. The Dragon Curve is often used to demonstrate fractal properties in mathematics and is popular in recreational mathematics due to its intricate and beautiful patterns. It has applications in computer […]

In this study, I explore Cesaro Fractal, generated by Grasshopper. Usually, it is not possible to code recursive algorithms in Grasshopper. With the help of the Anemone add-on, these fractal curves are easy to model. I studied similar fractal algorithms here before. This one is very similar to the Koch’s snowflake. The only difference (as far as I understood) is the side of the spikes. Koch’s Snowflake generates triangular spikes […]

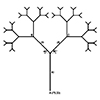
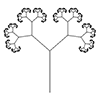
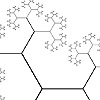
The Animated Tree Growth is an interesting study for Grasshopper. First, I developed a regular tree generation definition similar to those I studied earlier, here, here, and here. In component group 1, I develop an initial generator arc. Then, in group 2, I generate the fractal tree by using iteration. I did this with the help of the Anemone add-on. The interesting and original part of this definition is group […]

Here is a tattoo design I am currently developing by using Grasshopper. 11 years ago, I developed a Grasshopper definition that approximates Julia Sets here. One of the experimental outputs of that definition looks suitable for a tattoo design. It is a beautiful fractal shape. But I am not perfectly sure about its suitability for a tattoo. Here it is: This was generated by the function z2+c and the parameters […]

This is an implementation of the famous Koch Snowflake Fractal in Grasshopper. We will be using the Anemone add-on to handle the iterations. In this fractal, we start from an equilateral triangle. Then, we form new equilateral triangles, one-third of the side. So that each repetition protrudes in the middle of all the sides. In summary;1: Take a closed polygon and divide it into parts and divide each side into […]

Introducing the new YouTube channel for designcoding! The architectural Geometry playlist will contain video tutorials on several topics of basic geometry exercises for designers. Below are the introductory exercises of polyline drawing and some planar transformations such as scale and rotation. It is also an interesting plane-filling fractal you know I like it very much.

Anemone components are still working great, extending the abilities of Grasshopper. Here, I studied a space-filling (or plane-filling) fractal called the Gosper-Peano Curve. You should be very careful about the number of iterations (the N input). Because it can crash your Rhino if you change it to more significant numbers. Also, you should have Anemone components installed in order to run this definition. The generator curve is a special one. […]

We will see a simple Rhino Python exercise here. I called these Polygon Fractals (or Pentaflakes sometimes). It is both educational and fun to play with them. In Rhino, it can be a good exercise for basic CAD commands and transformations such as move, copy, and scale, and precision drawing operations such as object snapping. Also, in Grasshopper, it can be a good challenge for looping. In Rhino Python, it […]

A simple Rhino Python script that generates fractal curves. An example is a test with the Gosper-Peano curve. However the script is not supporting segment directions, which is why the result is not the intended curve. Curve directions could be implemented in the future. # Drawing Simple Fractal Curves # 31.07.2017 www.designcoding.net – Tugrul Yazar import rhinoscriptsyntax as rs import copy initials = rs.GetObject(“Select Initial Shape”,4) referenceA = rs.GetPoint(“Place Reference […]

This is a classical method of generating tree-like forms utilizing a simple command “Arc SED”. The idea is simple, as the command draws arcs using an input direction vector, so this could easily be implemented creating a “smooth” composition of curves just by iteration. Actually, this has been a previous study, discussed before here, using Hoopsnake. Now, this time I’m implementing the same algorithm using Anemone and a couple of other […]

Based on this post, the problem of modeling tree-like fractal shapes is still a good question for the early years of computational design education. Last time, I used Rhino’s macro to study these fractal trees in an “impossibly” limited interface. But this time I used a VB.net script. Here is the code inside of the VB.net component: Here are the inputs. x is the number of iterations. The Crv input is […]

Today’s design computing class was about fractals. In Rhino, writing macro statements are very easy to learn as it just mimics your behaviors in a sequential text. There are a few syntactic rules that we should know. First, you should watch the command line carefully to understand the steps of your design process. Each command in Rhino requires different inputs from the user. In macro, you may enter these values […]

Today’s fractal is the famous Mandelbrot Set. The Mandelbrot set is a well-known and complex mathematical set often associated with fractals and chaos theory. Named after the mathematician Benoît B. Mandelbrot, it’s a set of complex numbers defined by a simple iterative process. The Mandelbrot set is an intricate and self-similar boundary, which reveals increasingly complex patterns at different magnifications. On the other hand, I heard the term “The fingerprint […]