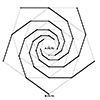
A spiral is a curve that begins at a central point and continuously moves outward, either getting larger (in an outward spiral) or smaller (in an inward spiral). It often revolves around a central point or axis. Spirals are fascinating because they appear in many aspects of nature, mathematics, and art. In this drawing exercise, I utilized several commands to draw such a system. However, this drawing is not a […]

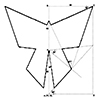
A fractal is a complex geometric shape that we can split into parts, each of which is a reduced-scale copy of the whole. This property is self-similarity. Fractals often exhibit patterns that repeat at different scales. We can find fractals in nature, such as in snowflakes, mountain ranges, trees, and clouds. We can also generate them mathematically. Fractals have applications in various fields such as physics, biology, and computer graphics. […]

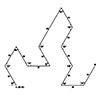
In mathematics, “curve” describes one-dimensional objects or line shapes, regardless of their curvature. Straight lines, polylines, and curved lines all fall under the category of “curves.” You may remember working with equation graphs in high school math classes. For instance, a first-degree equation produces straight-line graphs, while higher-degree equations, like “x squared,” create curved graphs. In this context, we focus on degree-1 curves, drawing straight-line segments using the polyline command. […]

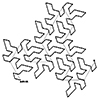
The Flowsnake, or Gosper curve is a space-filling fractal. It is also known as the Peano-Gosper curve. There are other similar space-filling fractals such as the Dragon curve, or the Hilbert curve. A space-filling fractal is a special type of curve, that fills a plane when iterated infinitely. This means, that if you continue to replace every segment of the polyline with the whole drawing, it will quickly become very […]

In computer-aided design (CAD), a polyline is a series (or a chain) of straight lines. Each straight section of a polyline is a “segment,” and the points where the segments connect are “vertices.” If a polyline’s starting and ending vertices coincide, it is a “closed polyline” or a “polygon”. If they do not, the polyline is classified as an “open polyline.” Polylines can be planar (2D) or 3D. The Gosper […]

Below is the first paper of my son, Mete Yazar. It is about a mathematical and geometric exercise of calculating the surface area of an arbitrary shape (a classical guitar’s body panel). He did a good job in utilizing Bezier/de Casteljau curves and generating the parametric equations of the piecewise curve. I helped him to validate the results by using rhinoceros CAD software. Therefore, it seems that his calculations are […]

Here is the shortest possible way of generating quick parametric curves in Rhino Python. So, you may change the f, g, and h functions to test any function curve. In this Python code, the list comprehension [(f(t), g(t), h(t)) for t in [t0 + i*dt for i in range(int((t1-t0)/dt)+1)]] works by first generating a list of t values from t0 to t1 with an increment of dt using the inner […]

Here is a wave generator code I developed using Grasshopper and Python. While searching for a solution to the realistic water simulations, I came up with the Gerstner Waves. I tried to implement it. However, I came up with this final result, which is not a Gerstner Wave generator, but a much simpler one. It combines many user-fed wave components and calculates the resulting single wave. I played with this […]

Today’s beautiful curve is the spherical cycloid. It is a cycloid, rolling on a 3d circular path rather than a straight and 2d one. There are algebraic explanations of this curve. Therefore, I find it interesting to experiment with them, since it is more interesting than the regular planar cycloids, epicycloids, and hypocycloids. This curve is believed to have been studied first by Jean Bernoulli in 1732. The interesting and […]

Gyroid is a popular triply-periodic minimal surface. Although it is a mathematical entity, designers and architects like its approximations very much. We used an interpretation of Gyroid in the rammed-earth structure: “Common-action Wall” in 2017. In that project, we utilized its spatial quality of dividing the space into two intertwining and symmetrical volumes. By making one of these volumes solid, I left the other void. So, in this tutorial, I […]

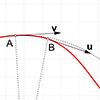
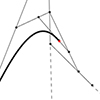
Curvature can be roughly described as how much a curve is “turning” at point a P. We place two “very” close tangents and measure the difference between them. The closer these tangents are, the more precise our approximation would be. An osculating circle is a tangent circle that has the same curvature as the curve at point P. The larger the circle, the more “flat” the curve is. An infinitely […]

Today’s computational curve is the beautiful Sierpinski Triangle. It is a fractal named after the Polish mathematician Waclaw Sierpinski, who described it in 1915, though it had been previously described by other mathematicians. It is a self-replicating pattern that arises from a simple recursive process. To construct the fractal, you start with an equilateral triangle and then repeatedly remove smaller equilateral triangles from its interior, leaving holes. Each iteration involves […]

Lissajous curves, named after the French physicist Jules Antoine Lissajous are a family of curves that emerge from the interaction between two harmonic oscillations. They have applications in various fields including physics, engineering, and signal processing. They are commonly used in electronic devices such as oscilloscopes to visualize the phase relationship between two oscillating signals. Similarly, they are also useful in mechanical engineering for analyzing and designing mechanisms that involve […]

This is a short video tutorial on the B-Spline decomposition I studied earlier here. This tutorial demonstrates how to decompose a B-Spline curve into Bezier curves using Rhino. Despite the original Bezier-de Casteljau algorithm requiring degree+1 control points, Rhino allows drawing a degree-3 curve with any number of control points. By examining knot points and dividing segments appropriately, the B-Spline curve can be manually subdivided into Bezier curves. This involves […]

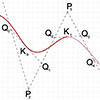
In this short tutorial, I am going to show you how to locate a parametric point on a Bezier curve. This will be a third-degree cubic Bezier curve. So, I start by placing four control points. I name these points from P0 to P3. Then, I connect them by a polyline in order. I explode the polyline into the segments. The parameter of my point must be a number between […]

De Boor’s algorithm, a maestro of basis spline refinement, meticulously navigates through knots, unraveling the intricacies of B-splines with mathematical precision. Meanwhile, De Casteljau, the geometric orchestrator, takes center stage in the Bezier ballet, elegantly guiding control points through a recursive dance. Together, these algorithms fuse art and mathematics, seamlessly sculpting curves and splines with technical finesse, creating a harmonious symphony of numerical intricacies in computational geometry. ChatGPT is so […]

The Hilbert Curve, also referred to as the Hilbert space-filling curve, was initially introduced by the German mathematician David Hilbert in 1891. It is a continuous fractal curve, presenting a variation of the space-filling Peano curves uncovered by Giuseppe Peano in 1890. After a study on the mathematical background of this curve, I implemented a Python code into Grasshopper Python. However, I wanted to explore more variations by playing with […]

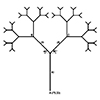
The Animated Tree Growth is an interesting study for Grasshopper. First, I developed a regular tree generation definition similar to those I studied earlier, here, here, and here. In component group 1, I develop an initial generator arc. Then, in group 2, I generate the fractal tree by using iteration. I did this with the help of the Anemone add-on. The interesting and original part of this definition is group […]

As the design of free-form architectural surfaces becomes easier, questioning and foreseeing the feasibility of the construction of these surfaces becomes important. Such an inquiry requires sufficient knowledge of architectural geometry besides the knowledge of materials and structural systems. In this article, we present a preliminary example of a guide. It supports the design and production process of building surfaces with different geometric properties is presented. This guide aims to […]

This Rhino Python code calculates the cross-product determinant used to determine the orientation of three points (current, next_point, and point) to see if they form a left turn or a right turn. This is a well-known technique in computational geometry to check the relative orientation of points. In this script, the direction is the cross-product determinant that determines the relative orientation of the points. If the result is negative, the […]