Using a compass and straightedge enables precise geometric constructions, allowing for the creation of complex tessellations. To begin these constructions, a single starting point is sufficient. Circles, which represent a collection of points at a specific distance from the center, and straight lines, which represent a collection of points in a particular direction, are utilized for geometric constructions. In this short tutorial, we move on with the beginner-level drawing exercises. […]

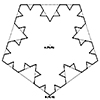
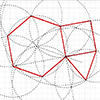
The Koch pentagon is a fractal shape that starts with a regular pentagon. Here, we divide each side of the pentagon into three equal parts. Then, we replace the middle with two sides of an outward-pointing equilateral triangle. We repeat this process for every new side in each iteration, creating a self-similar pattern. Helge von Koch (1870–1924) was a Swedish mathematician known for his analysis and number theory work. He […]

In geometry, “tangent” refers to a scenario where a line, curve, or surface touches another at exactly one point without crossing or leaving a gap. A tangent line to a circle is a straight line that touches the circle at only one point, and it is perpendicular to the radius at that point. Two circles can be tangent either internally or externally. Geometric constructions using a compass and straightedge can […]

The geometric shapes constructed using only a compass and straightedge have significantly influenced the development of reasoning and logic that underpin modern science. This non-numerical approach is also known as the Synthetic Geometry. Before René Descartes introduced Analytic Geometry, this method was widely studied and practiced. In “Elements”, Euclid explores fundamental rules, such as ‘The straight line between two points is the shortest,’ and derives all geometric truths from simple, […]

The practical geometry of the ancient Egyptian “rope-stretchers” delineated land after the annual flooding of the Nile River. Thus, the term “geometry” derives from the Greek words “gaia” (earth) and “metria” (measurement). Greek mathematicians used compass and straightedge to perform similar calculations on paper. This abstract thinking allowed for insights into the underlying logic, independent of the accuracy of hand tools. So, the abstract “circle” and “line” constructed by perfect […]

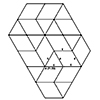
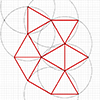
The rhombitrihexagonal tiling is one of the semi-regular tessellations. It is composed of regular hexagons, squares, and triangles. It is a periodic tessellation since you can copy the fundamental unit and move it across the plane to generate the tiling. I use this quality of the tiling to draw and expand it in Rhinoceros software. This is a basic drawing exercise. At the same time, it is a nice exercise […]

The snub square tiling is one of the semi-regular tessellations, where regular triangles and squares match perfectly to fill the plane without gaps or overlaps. The Euclidean construction of Snub Square tiling is possible by utilizing the basic compass and straightedge operations. I made this construction in Rhinoceros to show that there is no need for any numerical input to locate the points and draw the tiling. There are two […]

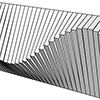
Santiago Calatrava, a celebrated Spanish architect, structural engineer, sculptor, and painter, is renowned worldwide for his groundbreaking and futuristic designs, which frequently fuse architecture with engineering and artistry. Among his many notable works is the door design at Ernsting Warehouse in Coesfeld, Germany, constructed in 1985. I call this Calatrava Door because this design showcases Calatrava’s keen sense of functionality and geometry, with aluminum slats arranged vertically and connected along […]

While digging through the lecture archive, I found this video I made in 2017. We introduce Platonic solids and Archimedean solids in the Design Geometry course at Istanbul Bilgi University. This video shows how we can create an Archimedean solid, the Truncated Tetrahedron, by folding it from a flat sheet.While doing this, I intersected the spheres by using the relations between the side lengths of the solid, and I calculated […]

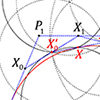
This is a new paper published in Nexus Network Journal. I tried to implement euclidean constructions by compass in the approximation of famous parametric curves; Bézier curves, and B-Splines. Then, I created the algorithms to calculate the number of steps on a compass-only construction of Bézier curves. I developed a simple Python script to simulate the geometric constructions. However, I have been studying this topic for nearly four years. In […]

This video shows the method of constructing equal segments on a line by only using compass operations. Here, you can see that there is a pattern in the number of required compass operations. For example, if you need to divide the distance by 3, you need 13 circles (or compass operations). This reveals a simple equation of c = 2 * n + 3 where n is the desired number […]

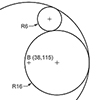
I learned this method from the open math resources website. I couldn’t help myself repeat it in Rhinoceros. It was quite fun to solve circle tangency problems in 2D, this is one of them: drawing the circle that passes three given points, not using ready-made commands but only geometric tools of the circle (compass) and ruler (line). Here is the sequence of it: First of all, we need to know […]

Here is a simple explanation of the famous Euclidean Constructions: Why didn’t Euclid just measure things with a ruler and calculate lengths? For example, one of the basic constructions is bisecting a line (dividing it into two equal parts). Why not just measure it with a ruler and divide by two?One theory is the the Greeks could not easily do arithmetic. They had only whole numbers, no zero, and no […]

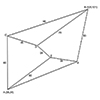
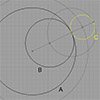
The first-year Architectural Geometry course includes Euclidean constructions as a study of associative geometry. We have exercised the below questions to study this topic. These are three mutually tangent circles, that can be drawn using only a compass and ruler, without built-in tangency functions in Rhino. Such exercises are expected to improve students’ reasoning. We believe architectural geometry education should encourage a conception that allows students to think about what […]