Here is the shortest possible way of generating quick parametric curves in Rhino Python. So, you may change the f, g, and h functions to test any function curve. In this Python code, the list comprehension [(f(t), g(t), h(t)) for t in [t0 + i*dt for i in range(int((t1-t0)/dt)+1)]] works by first generating a list of t values from t0 to t1 with an increment of dt using the inner […]

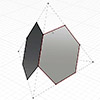
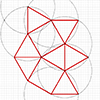
Modeling a rhombicosidodecahedron requires exploding and extending the faces of a dodecahedron and an icosahedron of the same edge length. We begin with both polyhedra centered at the same point. Then, we explode the faces of the dodecahedron and icosahedron outward from the center. We extend their planes while maintaining their orientation and shape. As these faces extend, they intersect and form new polygonal regions. Triangular and pentagonal faces emerge […]

It is not possible to cover a double curvature surface with planar quads. Here is one method that overcomes quad tiling on double curvature by pulling one vertex of the quads to the plane defined by the other three. This method was used in architecture on several occasions such as the exterior facade of The Yas Hotel, designed by Asymptote Architecture in 2009. The same approach is also evident in […]

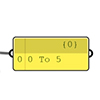
In this short tutorial, I am showing the essentials of data domains in Grasshopper. A domain is a data type in Grasshopper that represents a portion of the 1d or 2d number space. This requires a starting and ending point in those spaces. In 1d, these points are two numbers. Then, the domain represents all the numbers between them. In 2d, a data domain is represented by two coordinates (u, […]

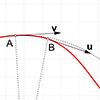
Curvature can be roughly described as how much a curve is “turning” at point a P. We place two “very” close tangents and measure the difference between them. The closer these tangents are, the more precise our approximation would be. An osculating circle is a tangent circle that has the same curvature as the curve at point P. The larger the circle, the more “flat” the curve is. An infinitely […]

Truncation refers to the process of shortening something by removing parts. You can apply truncation to numbers, text, or data in various contexts. A truncated polyhedron is a geometric solid formed by truncating the vertices of a regular polyhedron. Truncation involves cutting off the corners or vertices of the polyhedron in such a way that the original faces become polygons with new edges. This process creates new faces at the […]

The rhombitrihexagonal tiling is one of the semi-regular tessellations. It is composed of regular hexagons, squares, and triangles. It is a periodic tessellation since you can copy the fundamental unit and move it across the plane to generate the tiling. I use this quality of the tiling to draw and expand it in Rhinoceros software. This is a basic drawing exercise. At the same time, it is a nice exercise […]

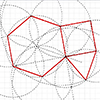
The snub square tiling is one of the semi-regular tessellations, where regular triangles and squares match perfectly to fill the plane without gaps or overlaps. The Euclidean construction of Snub Square tiling is possible by utilizing the basic compass and straightedge operations. I made this construction in Rhinoceros to show that there is no need for any numerical input to locate the points and draw the tiling. There are two […]

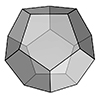
This is a 3d modeling tutorial for the platonic solid of dodecahedron. Modeling a dodecahedron is a good exercise for the basic transformation commands such as Rotate3D in Rhinoceros. You will see that it is possible to calculate the rotation angle by using sphere intersections. I learned this elegant method while teaching Architectural Geometry classes 12 years ago. It is based on the fact that, given a rotation axis and […]

This is a short video tutorial on the B-Spline decomposition I studied earlier here. This tutorial demonstrates how to decompose a B-Spline curve into Bezier curves using Rhino. Despite the original Bezier-de Casteljau algorithm requiring degree+1 control points, Rhino allows drawing a degree-3 curve with any number of control points. By examining knot points and dividing segments appropriately, the B-Spline curve can be manually subdivided into Bezier curves. This involves […]

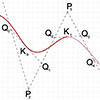
In this short tutorial, I am going to show you how to locate a parametric point on a Bezier curve. This will be a third-degree cubic Bezier curve. So, I start by placing four control points. I name these points from P0 to P3. Then, I connect them by a polyline in order. I explode the polyline into the segments. The parameter of my point must be a number between […]

Data structures and data matching principles are important to be able to design with #Grasshopper. In this tutorial, I show data matching procedures with arithmetic operations. Then I repeat them in the production of geometric objects. I think it should be easier to use this programming language once the students understand the basic principles. Therefore it would be easier to design with it. Sometimes the design process of these diagrams […]

The Truncated Icosahedron (5,6,6) is an Archimedean Solid we often recognize as the iconic soccer ball. This geometric structure, also affectionately known as the “Buckyball” in honor of the visionary architect Buckminster Fuller, has gained significant popularity and recognition both within the realms of mathematics and everyday life. It is composed of twelve regular pentagons and twenty regular hexagons, meticulously arranged to achieve a harmonious balance. This symmetrical nature makes […]

A Moebius strip, also known as a Moebius band, is a fascinating mathematical object and a type of non-orientable surface. It was discovered independently by the German mathematicians August Ferdinand Möbius and Johann Benedict Listing in the 19th century. To visualize a Moebius strip, imagine taking a long, narrow strip of paper and giving it a half twist before connecting its ends to form a loop. The result is a […]

Since the mid-20th century, the hyperbolic paraboloid surface has been one of the most popular mathematical forms for architects. Named Hypar in short, this is the Quadric Surface equation of the Hyperbolic Paraboloid. Erik Demaine summarizes several examples from architecture such as the roof of the Girls’ Grammar School in London (designed by Chamberlin, Powell, and Bonn), the Philips pavilion at the 1958 Brussels exhibition designed by Le Corbusier, and […]

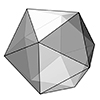
Today’s polyhedra is the beautiful icosahedron. It is one of the five Platonic Solids with twenty equilateral triangular faces. Its dual is the dodecahedron, which has pentagonal faces. Here, I explained the process of modeling an icosahedron. After creating a regular pentagon, you should find the “tip” point of the Icosahedron by intersecting spheres from at least three of the corner points with a radius of the pentagon’s edges. You […]

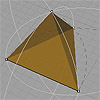
The tetrahedron is a platonic solid with four equal triangular faces (equilateral), six equal edges, and four vertices. In the construction of a tetrahedron, we will look closer at length transfers using compass-like tools in two- and three-dimensional space. To define the edge length of the first triangle, start with any two points in Cartesian space. Using a compass (arc or circle), draw two arches (or circles) using your initial […]