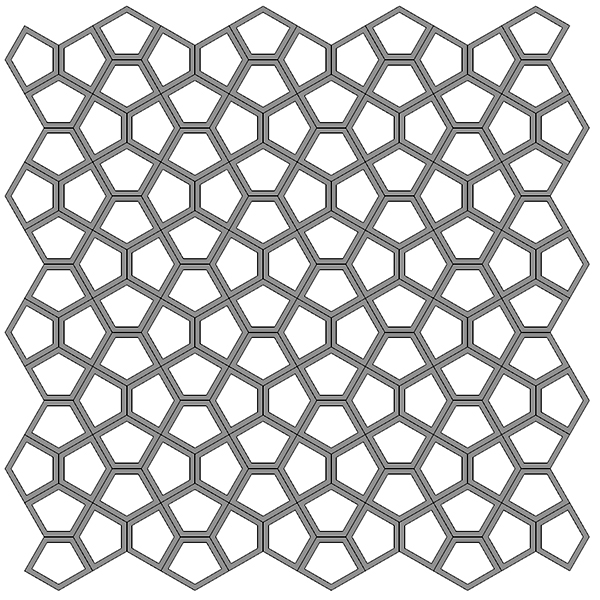
Cairo Pentagonal Tiling
This is a late update for my 2012 study on Cairo Pentagonal Tiling (or Cairo Tessellation). Originally, it was an exercise of dual tessellations. Because this tiling is the dual of the famous semi-regular tessellation of Snub Square. After coding the Snub Square tiling, I attempted to generate the dual of it. However, that created an inefficient result. This latest version generates the original Snub Square and Cario Pentagonal Tilings. Moreover, it is possible to play with the inputs to generate more interesting designs. The legend says that the name of this tiling comes from a special covering on the streets of Cairo. However, this doesn’t explain the origins of this very interesting pentagonal tessellation. There are an infinite number of pentagons that can tile a plane, obeying the same placement rule. This Grasshopper definition can be used to generate them.
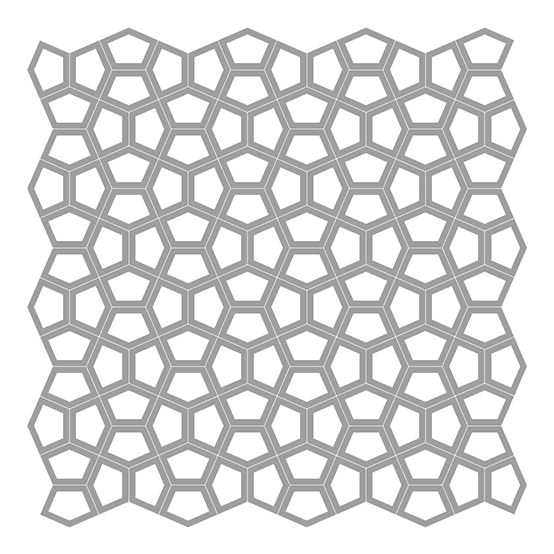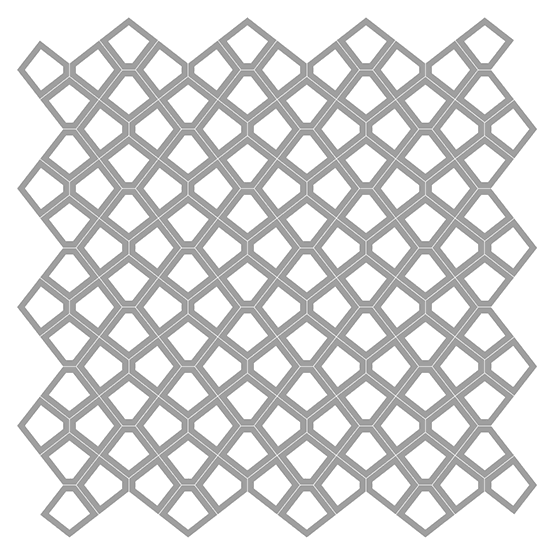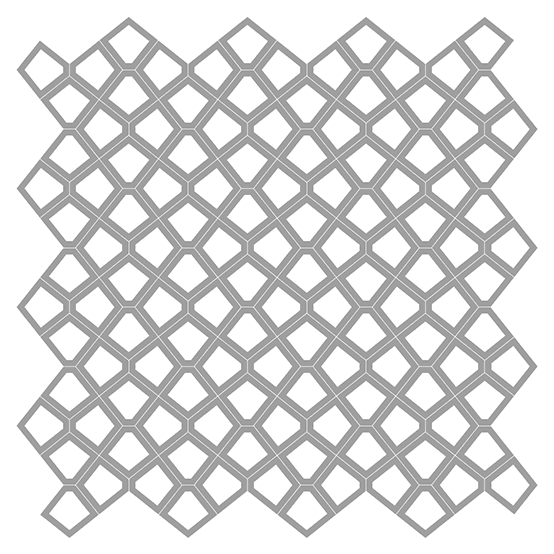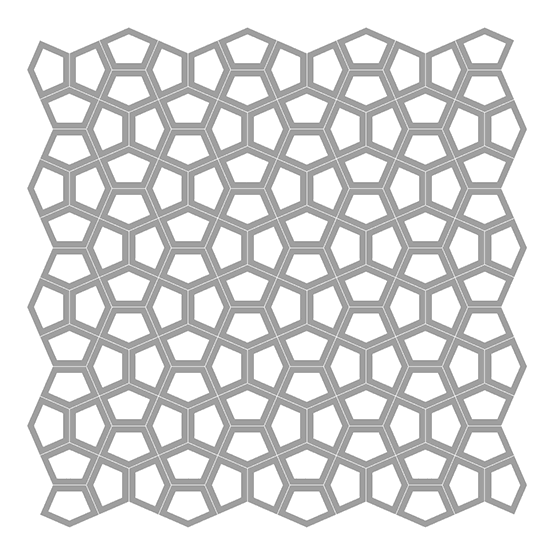
This Grasshopper definition generates variations of pentagonal mono tilings, including the famous Cairo Pentagonal Tiling. The input parameters are the rotation angle of the Snub Square base and the thickness of the resulting lattice. The output of the definition is the single-line tessellation and the closed polylines of the lattice. Therefore, the output is ready for manual cutting or laser cutting. The code is using native Grasshopper components. Thus, no add-ons are necessary for it to work.
Cite this post
Related Posts
Snub Square Tiling
October 22, 2012
Here is the step-by-step generation of the old Snub Square Tiling. Frankly, this is the first step in the generation of Cairo Pentagonal Tiling I generated with Grasshopper earlier. Because Cairo pentagonal is the dual of a snub square. The first step was easy. Just dispatch cells of a square grid, then evaluate them according to the ratio of 0.366 approx. which is derived from the bisector of an equilateral triangle. Now, we have a snub square tiling, composed of…
Scary Patterns
August 6, 2026
While digging through my archives, I found an old animation I made in 2023. Back then, I was generating patterns with Parakeet. Thanks to this talented add-on, I managed to create a nice pattern by dressing a different component onto a Snub Square tiling base. However, for some reason, things started turning into a horror movie after that. MultiPipe was popular back then. So, I converted this pattern into surfaces using MultiPipe and attempted an animation using Rhino’s rendered viewport…
Evolutionary Optimization of Tilings
April 19, 2025
In large-scale projects, calculating tiling layouts for wall, floor, and ceiling surfaces becomes even more critical. Evolutionary optimization of these tilings seemed to be a viable approach yesterday. Considering how time-consuming and labor-intensive this process can be, I tried using Galapagos, an old but often overlooked feature in Grasshopper, which might be particularly useful in this situation. Galapagos provides an alternative interface for evolutionary optimization within Grasshopper. It works by minimizing or maximizing a fitness value you define, using parameters…
Penrose Tiling Generator
April 16, 2024
A Penrose tiling exemplifies a type of tiling known as aperiodic. In this context, tiling involves covering a plane with non-overlapping polygons or shapes. Aperiodic means the tiling lacks arbitrarily large repeating sections. These tilings derive their name from mathematician and physicist Roger Penrose, who extensively studied them during the 1970s. Despite their absence of translational symmetry, Penrose tilings can exhibit both reflection symmetry and fivefold rotational symmetry. I created a simple Penrose Tiling Generator in Grasshopper. I used the…
Snub Square Surface
February 20, 2013
For the last 10 days, I’ve been searching for a proper algorithm for representing surfaces using planar shapes. It is obvious that triangulation is an answer but there is an interesting research topic of planar remeshing using shapes other than quads, hexagons, or any other regular polygons. Especially in computer graphics, such things refer to the optimization of models to decrease the load of GPUs. In the Grasshopper community, this has also been discussed and there is a great implementation…