Bezier Function Extractor

by Tuğrul Yazar | December 26, 2023 17:50

Today’s curve is the beautiful Bezier curve. A series of linear interpolations between the coordinates of control points describe a Bezier curve. So, I created a simple tool in Grasshopper called Bezier Function Extractor to experiment with this elegant construction.

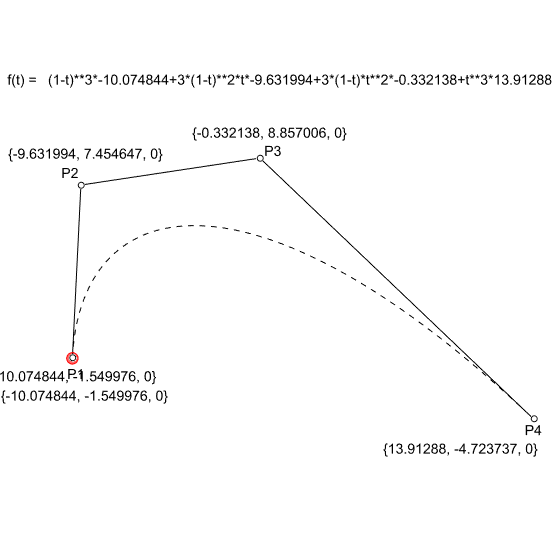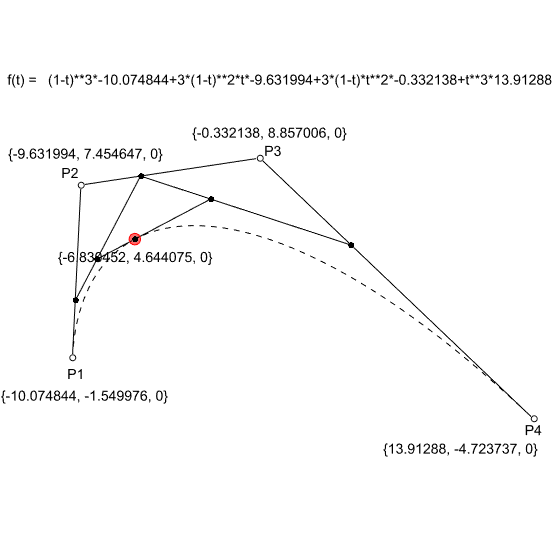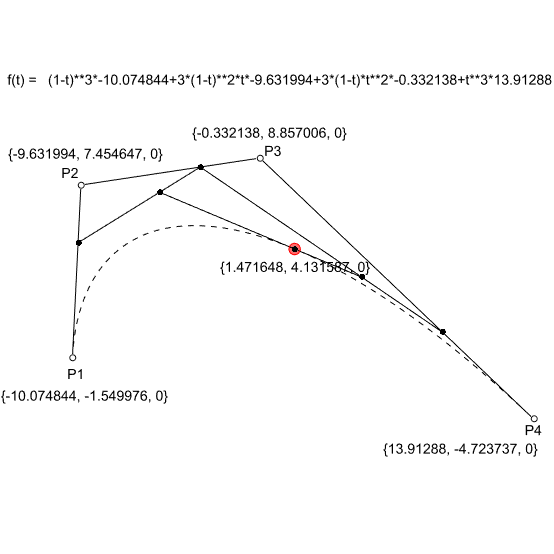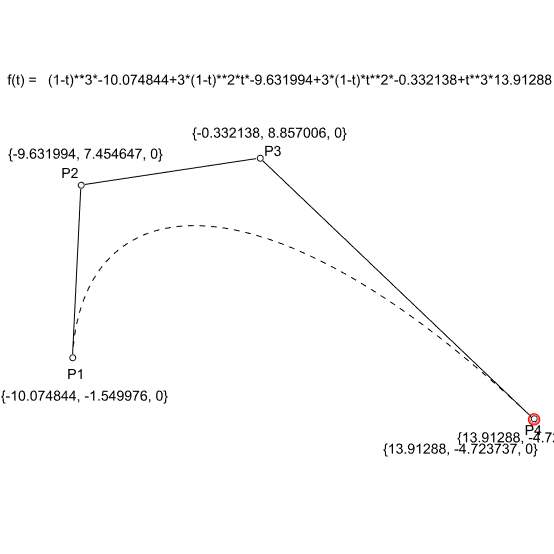
In the linear form (degree 1) the linear interpolation between 2 points (P1 and P2). The point at parameter t (0<= t <= 1); Q = tP1 + (1-t)P2. In the second degree, we need three points (P1, P2, and P3). The two linear interpolations between P1-P2 and P2-P3 would create two more points, Q1, and Q2. The resulting point on the Bezier curve is the linear interpolation between Q1 and Q2. Similarly, in degree 3 (mostly used degree in CAD) we need 4 points (P1, P2, P3, and P4). This time we repeat the same process three times to get the point at parameter t.

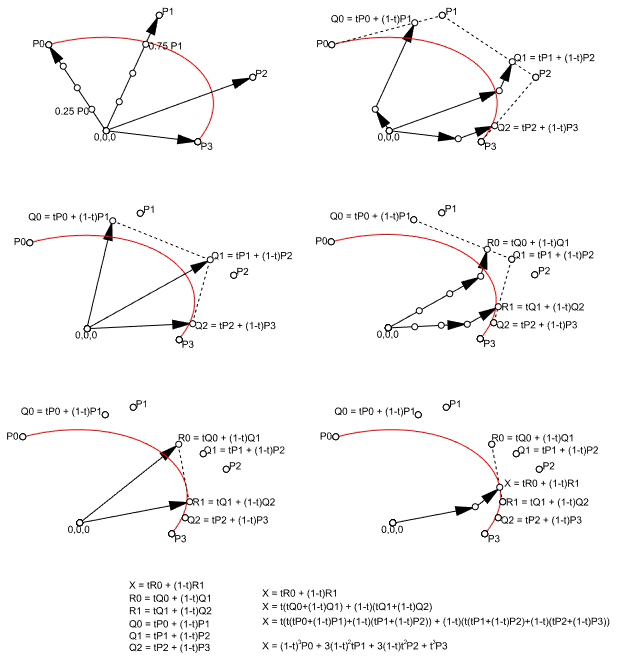
The above figure explains this process (Bezier – de Casteljau algorithm). Finally, below is the general formula that utilizes Bernstein polynomials and binomial functions to generate any degree Bezier function.

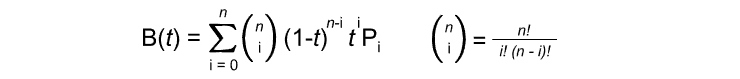
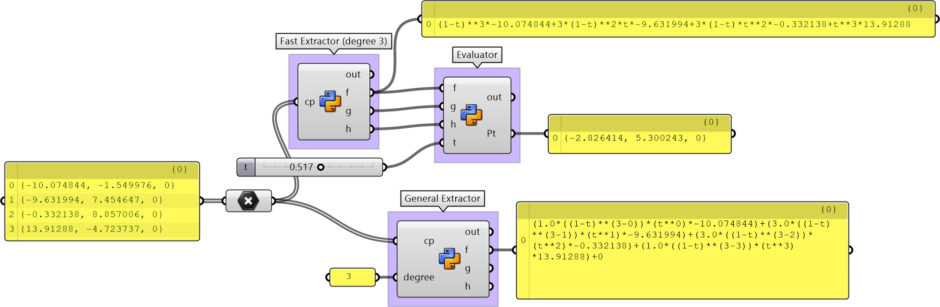
This Grasshopper definition gives the formula for the degree-3 Bezier curve with four given coordinates of the control points. There are three Python components in the definition. The first one is a fast degree-3 formula generator from the four points. It uses the coordinates of the four control points and outputs the x=f(t), y=g(t), and z=h(t) functions. Then, the second Python component is a General Extractor which generates the formula for any degree. The third one is an evaluator, showing the point on a given t parameter with given, f, g, and h functions. Therefore, it is proving the others and mimicking the function of the Evaluate Curve component in Grasshopper. I made the definition with the help of the native Grasshopper components in Rhinoceros 7. So, no external add-on is necessary.

[1]

You can check the de Castaljau algorithm in my previous post here[2]. However, if you want to support this website by downloading my working Grasshopper file[3] for Bezier Function Extractor, would you consider being my Patreon? Thank you.

Source URL: https://www.designcoding.net/bezier-function-extractor/

---