Today’s curve is the beautiful Bezier curve. A series of linear interpolations between the coordinates of control points describe a Bezier curve. So, I created a simple tool in Grasshopper called Bezier Function Extractor to experiment with this elegant construction.

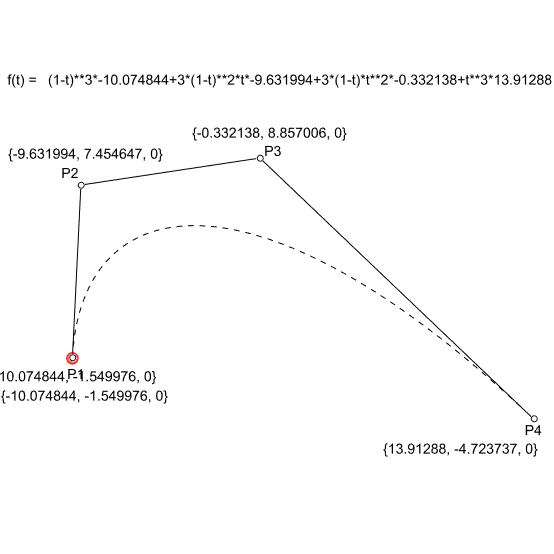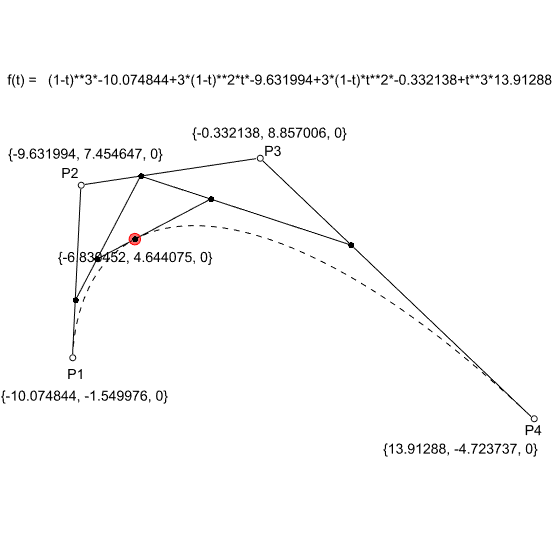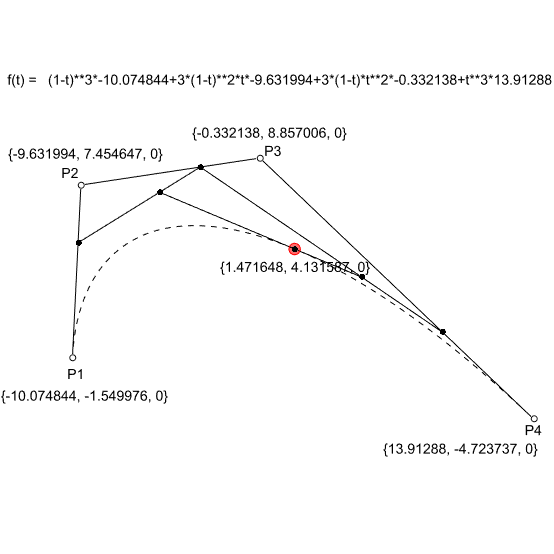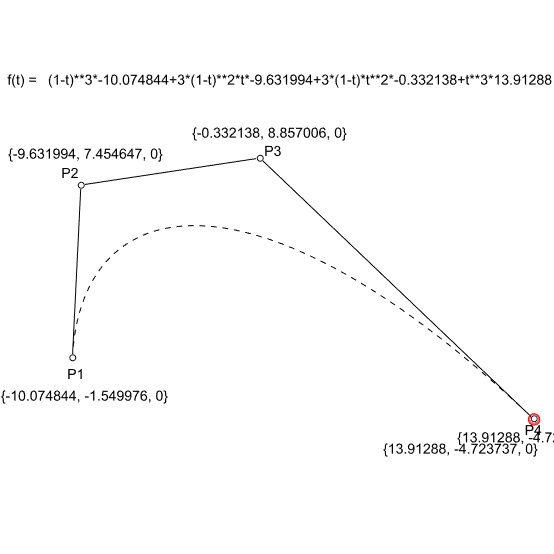
In the linear form (degree 1) the linear interpolation between 2 points (P1 and P2). The point at parameter t (0<= t <= 1); Q = tP1 + (1-t)P2. In the second degree, we need three points (P1, P2, and P3). The two linear interpolations between P1-P2 and P2-P3 would create two more points, Q1, and Q2. The resulting point on the Bezier curve is the linear interpolation between Q1 and Q2. Similarly, in degree 3 (mostly used degree in CAD) we need 4 points (P1, P2, P3, and P4). This time we repeat the same process three times to get the point at parameter t.

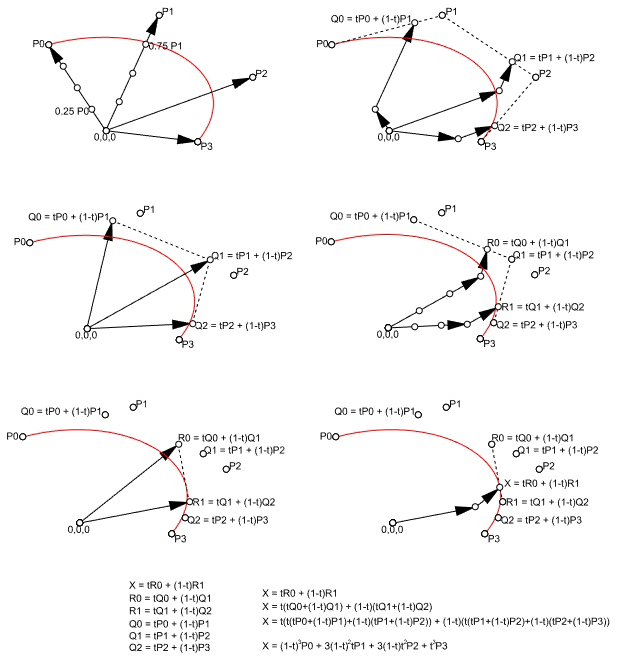
The above figure explains this process (Bezier – de Casteljau algorithm). Finally, below is the general formula that utilizes Bernstein polynomials and binomial functions to generate any degree Bezier function.

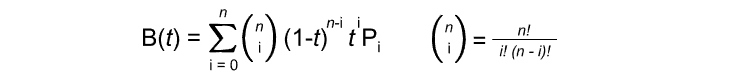
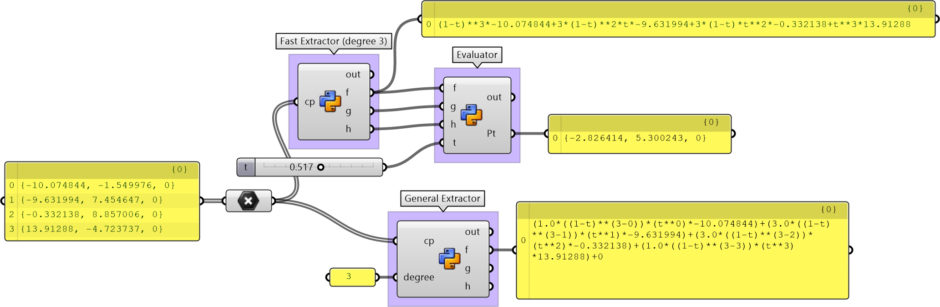
This Grasshopper definition gives the formula for the degree-3 Bezier curve with four given coordinates of the control points. There are three Python components in the definition. The first one is a fast degree-3 formula generator from the four points. It uses the coordinates of the four control points and outputs the x=f(t), y=g(t), and z=h(t) functions. Then, the second Python component is a General Extractor which generates the formula for any degree. The third one is an evaluator, showing the point on a given t parameter with given, f, g, and h functions. Therefore, it is proving the others and mimicking the function of the Evaluate Curve component in Grasshopper. I made the definition with the help of the native Grasshopper components in Rhinoceros 7. So, no external add-on is necessary.

You can check the de Castaljau algorithm in my previous post here. However, if you want to support this website by downloading my working Grasshopper file for Bezier Function Extractor, would you consider being my Patreon? Thank you.