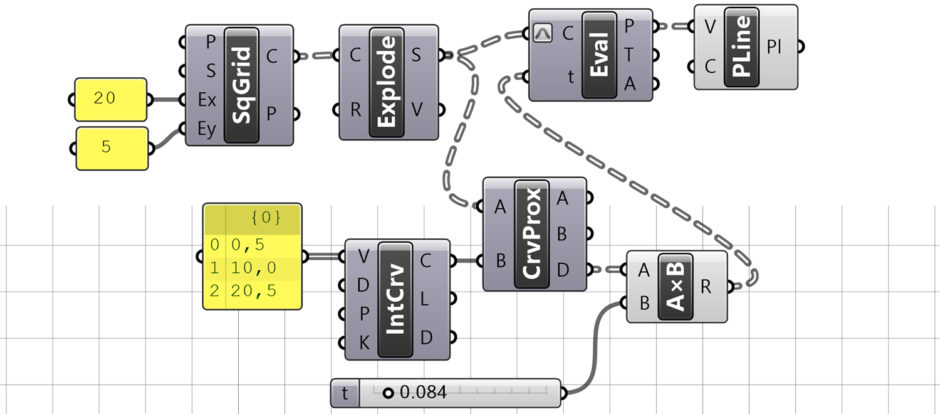
Basic Grid Deformation
I am still trying to find the simplest solution to some geometric definitions. This is why I called this Grasshopper definition “Basic Grid Deformation”. Here you see the Curve Proximity (CrvProx) component in use. This component calculated the shortest distance between two curves. I think the underpinnings of this component are very interesting. I hope I can code it in Python one day. In order to see the result more clearly, the Previews of the Interpolate Curve (IntCrv) and Square (SqGrid) components that we use are closed. As you can see, this definition shows the basic curve drawing to novice users. If you connect the distance (D) values from Curve Proximity (CrvProx) directly to the t input, the result will look complicated because the values are too high. Therefore, before sending the distance values to the Evaluate Curve (Eval), we multiply them by a number under our control and reduce them proportionally to absorb some.
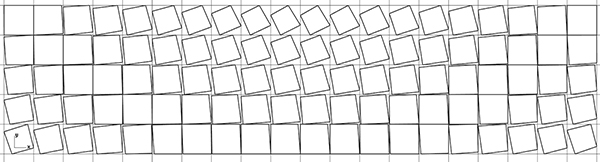
We could have done this reduction in other ways. For example, with the Remap Numbers (ReMap) component, we can scale a list of numbers from a given range to fit another range. We recommend that you try the same application in the same way. Let’s see if you can discover what other components you will need for the Remap Numbers (Remap) operation. Below is the diagram of the Basic Grid Deformation.
This definition is another basic exercise for beginners of Grasshopper. I hope it is beneficial for them. Here is the Grasshopper file, if you want to check it out:
Cite this post
Related Posts
Point Attractors Revisited
February 29, 2012
This is the basic definition of one point attractor on a grid of points. Here, the fundamentals of data tree matching can be studied. A hexagonal grid is exploded into points and new polygons are created there. Instead of a standard point distance relation to polygon size, this time the distance factor affects the rotational angle of these polygons. Although the structure of data trees is getting complicated, this has no difficulty in such definition, because the operational complexity is still very…
Minimal Parquet Deformations
January 28, 2013
Is it possible to model a two-way parquet deformation using only native components of Grasshopper? In this definition, I limited myself to 10 of them. Parquet deformations are a very interesting and pedagogical topic to teach some of the basics of contemporary parametric modeling. This post explains a minimal parquet deformations algorithm in Grasshopper. However, this has its own limitations. You will see that the definition generates the attractor graph curve. Because the graph input tool creates the magic here….
Inflating Grids
December 28, 2012
After playing with vector fields in 2d (here) it was quite easy to create a 3d surface deformation. Here is my first experiment on a regular triangular grid’s three-dimensional behavior within a vector space, that includes a point charge of varying z coordinates. That makes field lines escape to a bounding box, instead of a bounding rectangle. Again, you may play with force decay, the number of samples, and the “grid blast” parameter, which is just a t-value evaluation of…
Grid Tearing
January 6, 2012
Here, I used a curve to accomplish grid tearing. It’s straightforward, and from an educational perspective, this exercise includes several potentials on vector arithmetics and graph manipulation techniques. As a design domain, this definition stresses the use of associative entities in a parametric model. Any primitive or complex entity may evoke different parameters in others. The beauty in the simplicity of these algorithms still amaze me.
Point Waves
May 29, 2023
Here is another basic exercise in Grasshopper. This exercise “Point Waves” creates wave-like deformations on the grids of points. The major function of the definition is to calculate the distances from every point of a grid to an attractor point, with the help of Distance (Dist). Then it sorts them from the smallest to the largest (= closest to farthest) with the Sort List (Sort) component. This component takes and matches two lists of the same size, called key (K)…