B-Spline Construction

by Tuğrul Yazar | January 25, 2024 10:23

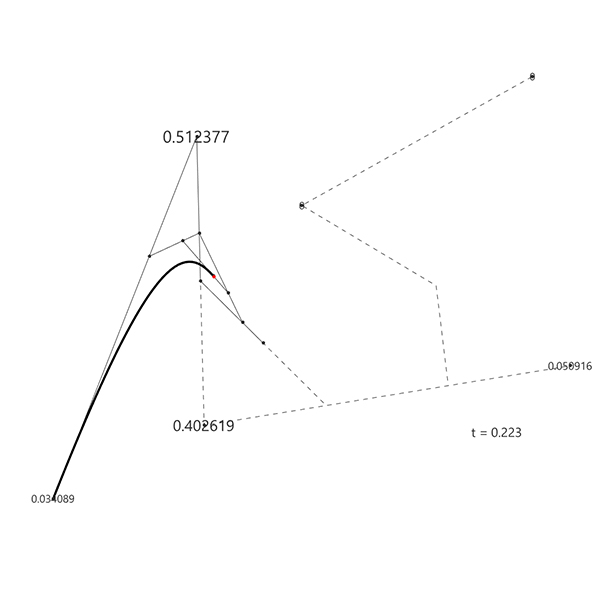
De Boor’s algorithm, a maestro of basis spline refinement, meticulously navigates through knots, unraveling the intricacies of B-splines with mathematical precision. Meanwhile, De Casteljau, the geometric orchestrator, takes center stage in the Bezier[1] ballet, elegantly guiding control points through a recursive dance. Together, these algorithms fuse art and mathematics, seamlessly sculpting curves and splines with technical finesse, creating a harmonious symphony of numerical intricacies in computational geometry. ChatGPT is so emotional today. I have been studying the Bezier-De Casteljau algorithm for several years. Last week, I finally managed to understand and implement B-Spline Construction in Rhino and Grasshopper Python code, using the Cox-De Boor algorithm. This algorithm calculates the effect of control points on a B-Spline with many control points. After this, I am not limited to the degree+1 control points. This animation shows both algorithms working together.

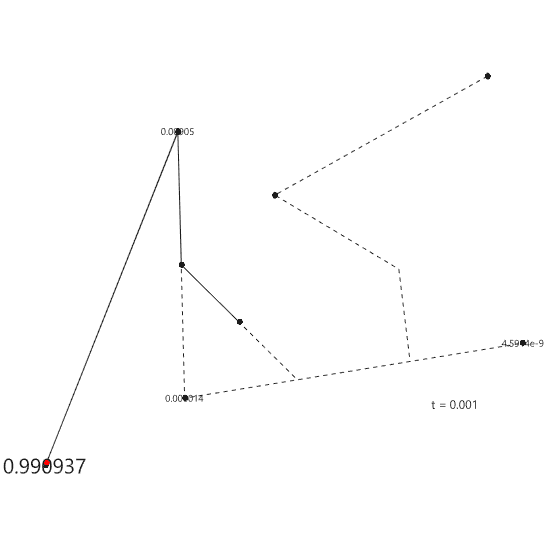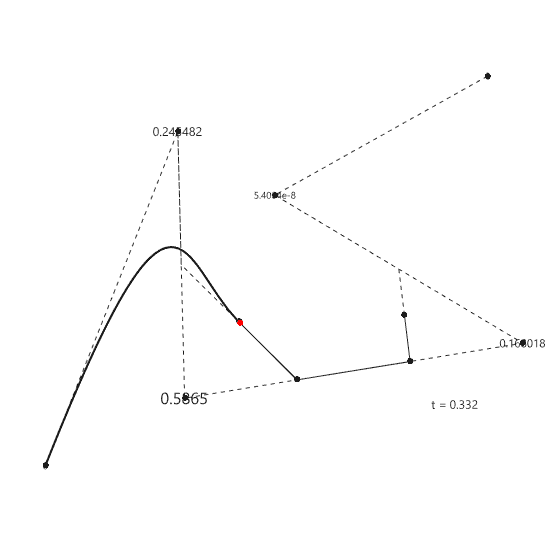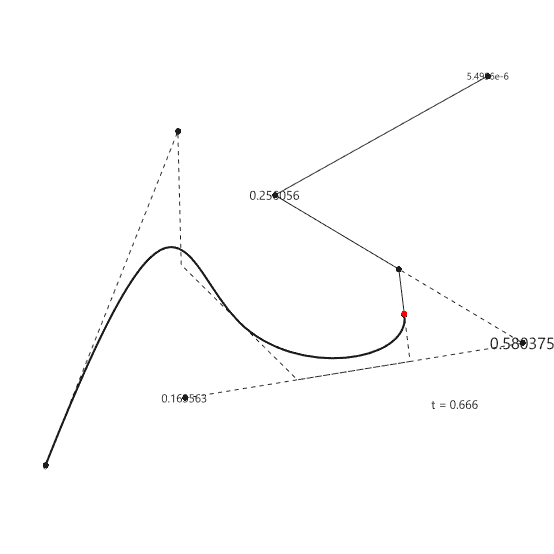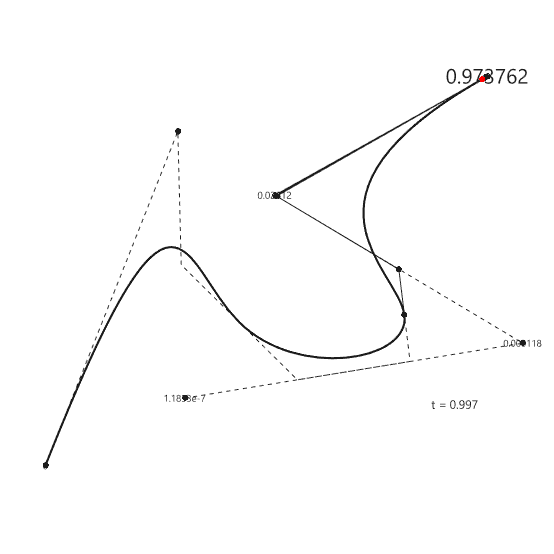
This Rhino Python code in a Grasshopper definition can handle three tasks. The first code draws a B-Spline with given control points and knot vector and degree. The knot vector is a list of numbers that controls many aspects of the process. The second code imitates the parametric evaluation so that a single point can be located on the curve. Finally, the third code handles and Bezier-de Casteljau algorithm and locates points on the Bezier curves with cp-1 degree.

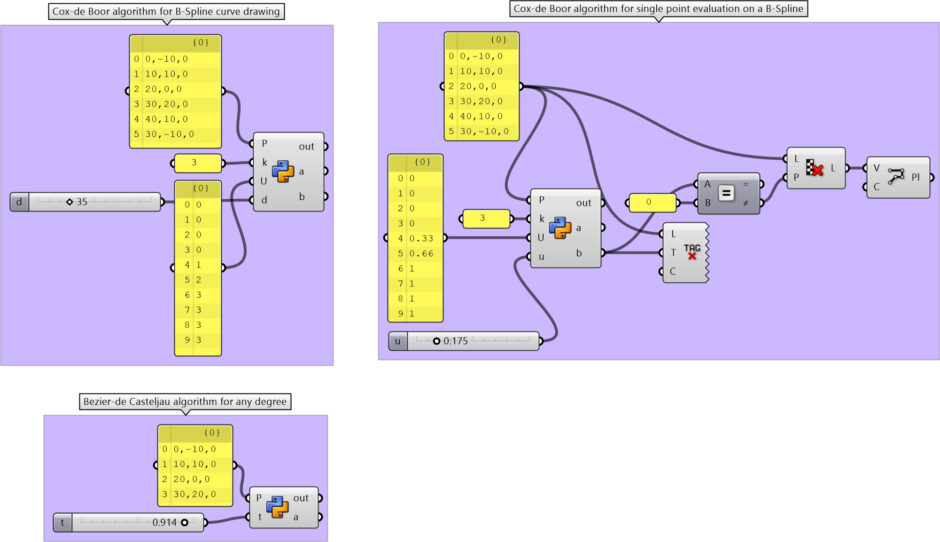
If you want to download and use the Grasshopper file; would you consider being my Patreon? Here is the link to my Patreon page[2] including the working Grasshopper file for the B-Spline Construction, and many more.

Source URL: https://www.designcoding.net/b-spline-reconstruction/

---