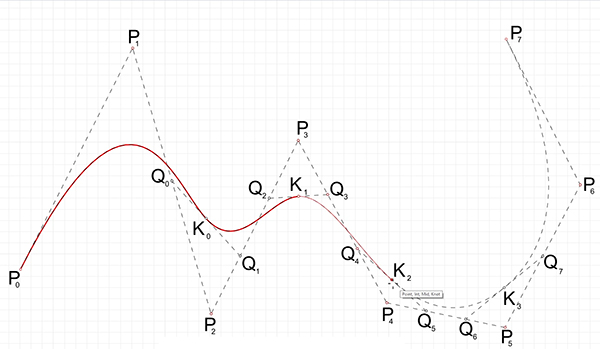
This is a short video tutorial on the B-Spline decomposition I studied earlier here. This tutorial demonstrates how to decompose a B-Spline curve into Bezier curves using Rhino. Despite the original Bezier-de Casteljau algorithm requiring degree+1 control points, Rhino allows drawing a degree-3 curve with any number of control points. By examining knot points and dividing segments appropriately, the B-Spline curve can be manually subdivided into Bezier curves. This involves placing control points, dividing segments, and connecting points in a specific order to reveal the Bezier spans. The tutorial emphasizes maintaining continuity and smoothness between segments through careful construction, ensuring tangency and curvature alignment at connecting points.

Guided by the tutorial, users embark on a systematic method. So, it begins with the identification of knot points along the B-Spline curve using Rhino’s Point command. These knot points serve as pivotal markers, delineating the curve into segments. Each segment represents a Bezier curve with four control points, in line with the degree-3 specification.

Throughout the B-Spline decomposition tutorial, I placed importance on preserving continuity and smoothness between segments. By connecting specific points in a prescribed order and ensuring collinearity and equidistance between certain points, users can seamlessly transition between Bezier curves while upholding essential principles of tangency and curvature continuity. Thus, this systematic methodology equips users with the knowledge and tools needed to effectively decompose complex B-Spline curves into smaller, more manageable Bezier segments, facilitating enhanced control and manipulation of curves within Rhino and other CAD environments. If you liked this content and want to support me for more, would you become one of my Patreons? Thank you.