Archimedean Spirals
by Tuğrul Yazar | December 17, 2012 11:40
In this exercise, Grasshopper draws various Archimedean spirals. It constructs polar points and maps them onto a range of angles and a number of points. The spiral’s turning speed is determined by the constant “a,” while the constant “n” gives unique names to the spirals by raising the angle variable to the power of 1/n. Wolfram Mathworld[1] names the spiral with n = -2 as lituus, n = -1 as a hyperbolic spiral, n = 1 as a regular Archimedes spiral and n = 2 as Fermat’s spiral. When viewed statically, these curves may seem boring, but Grasshopper brings them to life by animating the parameters and showcasing interesting natural movements. For example, the specific example provided shows a static sunflower (Fermat’s) spiral with an angle of 360, 100 points, a = 10, and n = 2.

Her is an animated archimedean spiral (angle = 360, number = 100, a is -10 to 10, n = 1)

The same parameters, this time animating number, fixing a = 10)

A hyperbolic spiral with a very small domain of angles = 3. Thus, it has 6 points performing break-dance with a constant increase on a (-10 to 10) and n = -1

Here is the definition if you want to play with it:
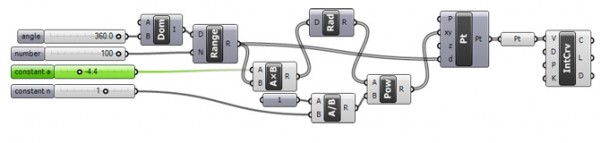 [3]
[3]Below is the “80’s style” hyperbolic spiral animation:
You can download the definition above. However, if you want to support this website by downloading my improved Grasshopper file; would you consider being my Patreon? Here is the link to my Patreon page[4] including the working Grasshopper files for the Archimedean Spirals and more.
- Wolfram Mathworld: https://mathworld.wolfram.com/ArchimedesSpiral.html
- Download: https://www.designcoding.net/decoder/wp-content/uploads/2012/12/2012_12_17-archspi.ghx
- [Image]: https://www.designcoding.net/decoder/wp-content/uploads/2012/12/2012_12_17-archspi-def.jpg
- Here is the link to my Patreon page: https://www.patreon.com/posts/archimedean-85185278?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
Source URL: https://www.designcoding.net/archimedean-spirals/