Approximating Gyroid

by Tuğrul Yazar | April 14, 2012 01:04

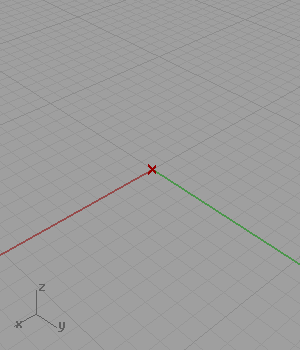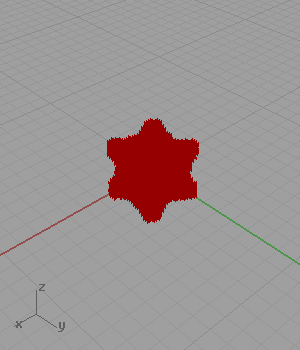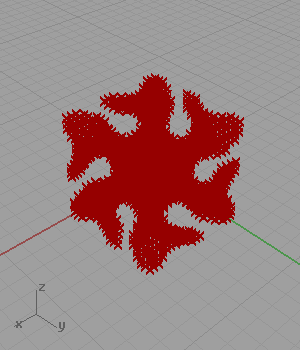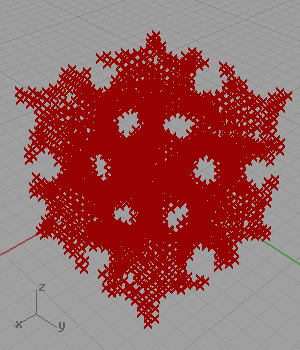
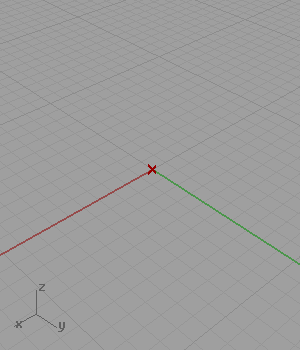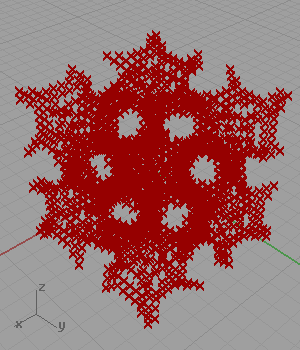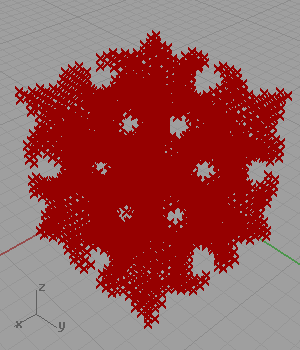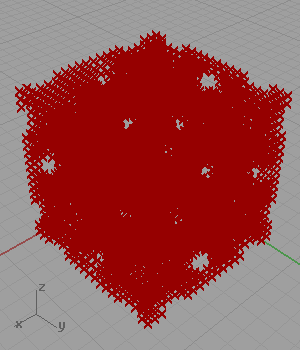
Another famous shape of architectural geometry is a set of definitions creating minimal surfaces. I’ve found the trigonometric equation of the Gyroid[1] and created a simple logic for approximating it as points in Grasshopper. However, when I searched the net for similar solutions, I found lots of them including the same approach as mine (Wynstan Wu’s definition). I was planning to develop a script in Grasshopper to take these estimated points and pull them to the Gyroid surface.

Then, I found that even there are people already done that as separate components in Grasshopper. This means, creating abstract geometric solutions for minimal surfaces is not an advanced problem, in contrast, it has become an introductory problem to be studied in basic education of computational design. As we know, abstract geometrical modeling is only one domain of a design mind. Other domains such as material and fabrication techniques are still to be studied at a more advanced level. This website[2] has a very good explanation of gyroid for dummies like me.

[3]

In my code for approximating Gyroid, I generated a three-dimensional grid of points. Then, I checked if the coordinates of any point is close enough to the following equation: cos(x)sin(y)+cos(y)sin(z)+cos(z)*sin(x). However, this 2012 definition is not working anymore. This is because of the fact that the Construct Point component does not create a 3D grid. I added a little randomness and fixed that issue in 2023. Below is the updated definition:

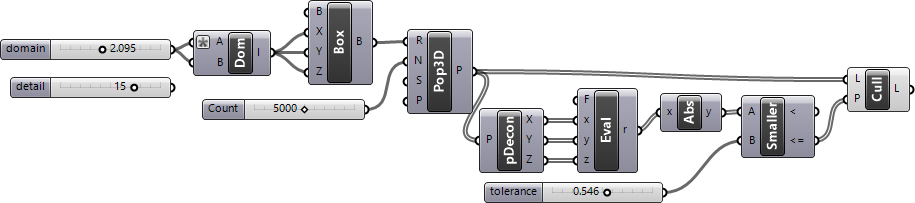[4]

You can re-build the definition by looking at the image above and the explanation. The “*” in the Domain component is “-x”. However, if you liked this content and want to download the Grasshopper file; would you consider being my Patreon? Here is the link to my Patreon page[5] including the working Grasshopper file for Approximating Gyroid.

Source URL: https://www.designcoding.net/approximating-gyroid/

---