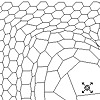
Fields is a native group of components available since the very early version of Grasshopper. In today’s Design Computing class, we studied it again with the first-year design students. I studied these interesting and beautiful shapes earlier here, here, here, and here. The one you see below is a short in-class exercise about vector fields. The exercise aims to show the Grasshopper’s capabilities in form-finding studies via Field Lines. The […]

In this session, I will add two new methods to the Vector class. I think this will finish the basics for the vectors. In the future, we are going to need several new methods like adding multiple vectors and interpolation. But for now, I think this would be sufficient to further advance into parametric curves and surfaces. These new methods will be based on the dot product method we created […]

This is the continuation of the Vector class we started here, and further advanced here, here, and here. This new Rhino Python implementation is mostly educational and partially a hobby. Before this session, we have developed display, magnitude, add, multiply, reverse, and subtract methods. This time, I am adding the vector normalization and dot product methods and seeing the utilizations of the dot product. Line Explanation 1-26 Already explained in […]

Today, I am going to make only one addition to the Vector class we recently started in Rhino Python. The magnitude of a vector can be easily calculated by assuming that the axes (2 or 3 axes) of it are perpendicular to each other. This gives us an opportunity to assume a right triangle visually, and calculate the magnitude (length) of a vector by using the Pythagorean Theorem. In short, […]

This is the continuation of my new project of re-creating the parametric curve and surface methods of Rhino via Python scripting. If you remember, I started with the building block of vector operations, here and here. Then, I defined vector addition and multiplication, before going deeper into the geometric calculations. In fact, they are using the previously defined addition and multiplication methods. New Vector Operations: Subtraction and Reversing In the […]

Today, I am going to advance the Vector class a bit more. Firstly, I will improve the display method I introduced recently. Then, I will add two new methods which handle the fundamental vector arithmetics in Rhino Python. Improving the Display Method In the previous attempt, I displayed vectors on the origin of the Rhino viewport. The coordinates of the tail of a vector are not stored within the object […]

Let’s continue from the Vector class that started yesterday. Previously, I defined this class to store three numbers (coordinates), named as “components”. I defined a method named __init__ for this. Similarly, I am adding a display method to the Vector class today. Note that I am using Rhino 6 in this code, but it should also work in Rhino 5 or 7. The code Below is the line-by-line explanation of […]

In this new series, I will be using Rhino Python to create some of the fundamental mathematical objects in Rhino. We will learn how to code in Python, and also try to get deeper into the intuition behind some of the fundamental concepts we use every day in Rhino and Grasshopper. The Vector class in Rhino Python is the starting point of this journey. Just like vectors, most of the […]

Utilizing “Force Field” components of Grasshopper to show my students how it is easy to develop flexible surfaces in design. The classical parametric canopy design is introduced in this video: According to Wikipedia; In vector calculus, a vector field is an assignment of a vector to each point in a subset of space.[1] A vector field in the plane, for instance, can be visualized as a collection of arrows with […]

Back to the basics. I finally had time to test the vector fields components in Grasshopper. It was a couple of updates ago, a new tool group emerged in the vector tab, introducing different types of vector fields to users. Then, these fields could be merged to form more complex effects. However, I created a very simple example of how we can use those components to distort a system (such […]

The regular dodecahedron is one of the five Platonic solids, characterized by having 12 regular pentagonal faces, 20 vertices, and 30 edges. When you elongate it, you extend its structure in one or more directions, resulting in a shape that retains the basic properties of the dodecahedron but is stretched out. The elongated dodecahedron might not catch your eye at first—it’s just a long version of a shape you’ve probably […]

The rhombic dodecahedron is a polyhedron with twelve rhombus-shaped faces, where each face has four sides of equal length. It is possible to construct the space-filling variant of the rhombic dodecahedron by arranging multiple such rhombic dodecahedra in a regular pattern so that they fill space without leaving any gaps. In his 1611 work on snowflakes titled “Strena seu de Nive Sexangula,” Johannes Kepler observed that honey bees utilize the […]

Stellated polyhedra are three-dimensional geometric shapes formed by extending the faces of a regular polyhedron (a solid with flat faces) beyond their original boundaries until they intersect with each other. The term “stellate” comes from the Latin word “stella,” meaning star and these polyhedra often have a star-like appearance due to their extended faces. They are popular because of their aesthetic qualities. I studied these forms many times before. This […]

De Boor’s algorithm, a maestro of basis spline refinement, meticulously navigates through knots, unraveling the intricacies of B-splines with mathematical precision. Meanwhile, De Casteljau, the geometric orchestrator, takes center stage in the Bezier ballet, elegantly guiding control points through a recursive dance. Together, these algorithms fuse art and mathematics, seamlessly sculpting curves and splines with technical finesse, creating a harmonious symphony of numerical intricacies in computational geometry. ChatGPT is so […]

In 2016, archi-union architects and fab-union intelligent engineering completed the renovation of the art gallery in Shanghai, China. The distinctive feature of the building was the robotic masonry fabrication of the brick facades. The undulating and waving parametric bricks were increasingly becoming popular after the introduction of parametric design tools such as Grasshopper and the works of Gramazio & Kohler at ETH Zurich since 2008, I guess. I made two […]

Perlin noise is a gradient noise function that has been widely used in computer graphics, procedural generation, and various other applications to generate natural-looking patterns. Here is my brief exploration of the Perlin Noise Generator. Although I didn’t fully follow the traditional steps the result looks similar. I started with the square grid and generated random gradient vectors on every grid corner. Then, I implemented the original algorithm’s dot product […]

Here is a short tutorial on getting help from Grasshopper in physical terrain modeling. It is a classical architectural terrain modeling process. Let’s see how Grasshopper can help us with this. Part 1: Terrain modeling for Laser cutter The terrain model entered in the Brep data store in this application is a closed/solid model. For now, you can also use ready-made components such as Cone or Sphere (Sph) to quickly […]