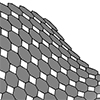
The intricate harmony of the Islamic Patterns is amazing. The geometry of this and other Islamic pattern designs are explained in the 3rd chapter of Craig S. Kaplan’s Ph.D. dissertation. I constructed a semi-regular tessellation, particularly the 4.8 because it seems to open interesting explorations that mostly emerge from truncated squares. We know equilateral triangles and hexagons are also fundamental shapes for this task. However, the dual nature of the […]

Truncated hexagonal tessellation (or named 3-12-12) is represented in hyperbolic space (as far as I understood it). The idea is simple if you don’t mix it with complex equations. Below is the 2-dimensional representation of hyperbolic projection. Paper space is defined by the thick line there. Projection is based on a two-sheet hyperboloid surface. Euclidean version of this tessellation is described here. Here is the Grasshopper3D file containing the above […]

Creating and handling new types of grid configurations might be an important topic, as Grasshopper is not supporting them natively (yet). I tried to create some semi-regular tessellations based on regular grids. It is actually truncated versions of regular grids, but it slowly becomes interesting as I realized that I may further truncate emerging grids to create Level 2 and Level 3 grids with more complex tessellations. Here are two […]

This is a semi-regular tessellation of vertex arrangement 4.8.8. Its octagonal and square forms are all generated from data lists provided by the new version of subdivide component (The old one was processing points in a different fashion. I don’t know why they changed that). Anyway, a lexical operation is needed to convert this list into a more useful one for this exercise. You can download the source definition here […]

Relief in the context of art and sculpture refers to a technique where a three-dimensional form is created on a flat surface. The object or figure “protrudes” from the background, creating depth and texture. In this short tutorial video, I am modeling waves relief using the basic drawing and modeling commands of the Rhinoceros software. Here, I use the point surface command. Because, in Rhinoceros, generally we describe the parametric […]

Truchet patterns refer to a set of geometric designs based on simple, repeating shapes, usually tiles or squares. These tiles can be rotated or flipped to create complex and visually interesting patterns. A French mathematician, Michel Truchet introduced these patterns in the 1970s. Since then, you can see them often in art, design, and mathematics. In this short video tutorial, I am modeling truchet relief in Rhinoceros CAD software. My […]

A “hypar” is short for a hyperbolic paraboloid, a double-curved, saddle-shaped surface often used in architecture and structural design due to its unique geometric properties. It is a ruled surface, meaning it can be constructed entirely with straight lines, despite its curved appearance. In this short tutorial video, I am building a beginner-level 3D pattern that resembles the hypar surface. This is a basic drawing exercise to control the viewport […]

In art, design, and geometry, folding involves bending or creasing a material—such as paper, fabric, or other flexible substances—into defined shapes or patterns. Folding techniques can also be used to create multidimensional forms and structures, blending artistic expression with practical functionality. In this short tutorial video, I am modeling a folds relief pattern. This pattern stands out due to its resemblance to a collapsible folding system, combining both structural and […]

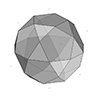
In geometry, a truncated icosidodecahedron, rhombitruncated icosidodecahedron, great rhombicosidodecahedron, omnitruncated dodecahedron, or omnitruncated icosahedron is an Archimedean solid. It is one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces. In this short tutorial, I am constructing an irregular truncated icosidodecahedron. It is not the regular Archimedean solid, but a rough approximation of it. I made this model to exercise the exploration of […]

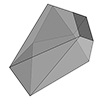
The sphenoid hendecahedron is a unique and interesting polyhedron. As the name implies, a “hendecahedron” is a polyhedron with 11 faces, while “sphenoid” refers to a specific type of shape that is often unusual, asymmetrical, and typically wedge-shaped. This polyhedron fills space, packing 3D space without gaps or overlaps. Its convex shape allows it to tessellate efficiently. Therefore, space-filling polyhedra play a crucial role in understanding tessellations and geometric arrangements, […]

The rhombicosidodecahedron, an Archimedean solid, is one of the 13 convex polyhedra made up of regular polygons. While all its faces are congruent, they consist of various types of regular polygons. I previously explored this fascinating polyhedron and am revisiting it now as part of the Architectural Geometry course. In this short tutorial video, I demonstrate the modeling of a rhombicosidodecahedron. Despite its lengthy and unusual name, this polyhedron is […]

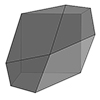
The Herschel nonahedron is a canonical polyhedron whose skeleton is the Herschel graph. It has 11 vertices, 18 edges, and 9 faces. Of the edges, 6 are short and 12 are long. It is characterized by having nine faces (hence the prefix “ennea” meaning nine in Greek). In this short tutorial video, I am folding Herschel’s enneahedron. To do that, I am constructing the interior angles of this polyhedron using […]

In geometry, the excavated dodecahedron is a star polyhedron that looks like a dodecahedron with concave pentagonal pyramids in place of its faces. In this short tutorial video, I am modeling an excavated dodecahedron in the Rhinoceros software. I use basic drawing and modeling commands. I aim to introduce this skill to beginner-level architects and designers. As the name suggests, this process includes the construction of the dodecahedron first. Then, […]

A truncated cuboctahedron is an Archimedean solid, meaning it is a highly symmetrical, convex polyhedron with identical vertices and faces of regular polygons. As its name suggests, you can create the truncated cuboctahedron by truncating (cutting off) the vertices of a cuboctahedron. A cuboctahedron is a rectified cube. After you model it, you can divide all its edges into 1/3s. Then, connect those division points to draw the squares, hexagons, […]

An icosidodecahedron is a polyhedron that is part of the family of Archimedean solids. It has 32 faces, consisting of 12 regular pentagonal faces of a dodecahedron and 20 regular triangular faces of an icosahedron. It is highly symmetrical, with the same arrangement of faces around each vertex. In this short tutorial video, I am modeling and unrolling an icosidodecahedron. This polyhedron is very interesting and is mostly used as […]

Stellation of polyhedra refers to the process of extending the faces (or edges) of a polyhedron outward to form new, more complex shapes. These new shapes, called stellations, are created by adding extra vertices, edges, and faces that “project” outward from the original polyhedron’s structure. You can create an infinite number of new polyhedral forms, depending on how you extend the faces and edges. In this short tutorial video, I […]

A dual polyhedron is a concept in geometry where two polyhedra are related in such a way that the vertices of one polyhedron correspond to the faces of the other, and the faces of the first polyhedron correspond to the vertices of the second. The process of creating a dual polyhedron is called duality, and it applies to many regular, semi-regular, and some irregular polyhedra. In the case of Platonic […]