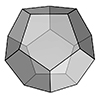
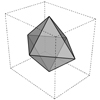
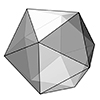
Here is a method for coding the dodecahedron and all its irregular variants in Grasshopper as quickly as possible. I utilized the golden ratio rectangles, usually used to construct the sister polyhedron, the icosahedron. However, the magic component of the Grasshopper, the Faceted Dome rescued me again to generate the dual of it, the dodecahedron. This is a special platonic solid, which has 12 regular pentagonal faces. There are several […]

The regular dodecahedron is one of the five Platonic solids, characterized by having 12 regular pentagonal faces, 20 vertices, and 30 edges. When you elongate it, you extend its structure in one or more directions, resulting in a shape that retains the basic properties of the dodecahedron but is stretched out. The elongated dodecahedron might not catch your eye at first—it’s just a long version of a shape you’ve probably […]

This is a 3d modeling tutorial for the platonic solid of dodecahedron. Modeling a dodecahedron is a good exercise for the basic transformation commands such as Rotate3D in Rhinoceros. You will see that it is possible to calculate the rotation angle by using sphere intersections. I learned this elegant method while teaching Architectural Geometry classes 12 years ago. It is based on the fact that, given a rotation axis and […]

While digging through the lecture archive, I found this video I made in 2017. We introduce Platonic solids and Archimedean solids in the Design Geometry course at Istanbul Bilgi University. This video shows how we can create an Archimedean solid, the Truncated Tetrahedron, by folding it from a flat sheet.While doing this, I intersected the spheres by using the relations between the side lengths of the solid, and I calculated […]

Today, we have studied creating complex robot programs manually again. Platonic solids were the subject of this study. Students tried to create a sequence of robot moves that produces a Platonic solid out of a 17cm EPS cube. We simply call this the robotic hotwire cutting polyhedra exercise. However, the size of our hotwire cutter became one of the problems because of its risk of crashing. We crashed several times […]

According to Wolfram, “By the duality principle, for every polyhedron, another polyhedron exists in which faces and polyhedron vertices occupy complementary locations. This polyhedron is known as the dual, or reciprocal”. We can use this method to generate new polyhedra from known ones. I tried to develop a Dual Polyhedra Generator in this Rhino Python script. First, the script asks a user to select a closed polysurface object. Then, it […]

This is the second year we are experimenting with a beautiful exercise with the Computation-based Basic Design 1 students at İstanbul Bilgi University Faculty of Architecture. The exercise is based on the ideas of Benay Gürsoy and Şebnem Yalınay, who are among the pioneers of this studio. The exercise is about the design and production of new year’s lanterns to be lit in the campus garden. Here are a few […]

Today’s Architectural Geometry course was about platonic solids and different attractor objects in introducing component-based design systems. Benay’s idea was both pedagogical and interesting to test in Grasshopper. I searched for the most fundamental type of attractor solid in creating a composition such as this; There is a subdivided sphere and an attractor sphere. The pull component works great here. You may use multiple attractor solids or different shapes such […]

I have come across several high school topics I was afraid of. While I was searching for a geodesic dome definition in Grasshopper, it was quite surprising that I found an easier way of modeling an approximation of icosahedron, the famous platonic solid. Icosahedron was a research topic of this website at various posts before (here, here, and here). In order to generate geodesic spheres, first I had to solve […]

Not all of them, but when you get the idea, you’ll see there are lots of different alternatives for creating Fuller’s famous Geodesic Domes (Although in fact, he is not the inventor of it). I was playing with Platonic Solids in Rhino and realized that the “Pull” command is very useful in subdividing objects. I modeled this in Rhino 4. First, take a regular Icosahedron and divide it. Because, this […]

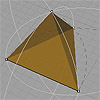
The tetrahedron is a popular platonic solid for designers. We’ve explained how to draw them using equilateral triangles here before. Recently I’ve found (sorry, lost the web address) a much quicker way of modeling a Tetrahedron using a cube. It’s very simple, just connecting the three opposite corners of the cube automatically makes them equal, resulting in the four equal faces. Of course this time you’ll have to calculate the […]

I tried different approaches to drawing platonic solids using Grasshopper’s native components. However, it seems impossible now. In geometric definition, a platonic solid is a set of points, distributed on a sphere with equal distances. If the set contains 12 points, then it’s an icosahedron. I found lots of information about these objects and mathematicians seem to love analyzing them. They created different approaches to building an icosahedron. One of […]

An octahedron is a polyhedron and platonic solid with 8 faces of identical equilateral triangles. In this post, I will try to explain the drawing and unrolling process of the octahedron. It has a close relationship with the cube as it’s dual. In order to construct an octahedron, we first have to create a square. The main problem of drawing the square is determining the right angle (perpendicular axis) to […]

The dodecahedron is a Platonic Solid with 12 equilateral pentagonal faces. It has a close relationship with its 20-sided dual, Icosahedron. Mete Tüneri showed the following method of Dodecahedron construction, using only distances, corners of the pentagon, and a visionary equilateral triangle underneath. We’ll construct Dodecahedron, assuming that we’ve drawn an initial equilateral pentagon. We need to find out the pentagon’s angle of 3d rotation. First, put spheres at points a […]

Icosidodecahedron is an Archimedian Solid, a thing in between the Platonic Solids of Icosahedron (d20) and Dodecahedron (d12). It is a rectified version of an Icosahedron, constructed by dividing every edge into two equal segments and joining these segments to create a composition of equilateral pentagons and triangles. Archimedian Solids consist of at least two equilateral polygons, whereas Platonic Solids are constructed by only one. We’ll deduce an Icosidodecahedron from […]

Today’s polyhedra is the beautiful icosahedron. It is one of the five Platonic Solids with twenty equilateral triangular faces. Its dual is the dodecahedron, which has pentagonal faces. Here, I explained the process of modeling an icosahedron. After creating a regular pentagon, you should find the “tip” point of the Icosahedron by intersecting spheres from at least three of the corner points with a radius of the pentagon’s edges. You […]

The tetrahedron is a platonic solid with 4 equal triangular faces (which are also equilateral), 6 equal edges, and 4 vertices. While creating this shape, we will take a closer look at length transfers using compass-like tools both in two and three-dimensional space. In order to define the edge length of the first triangle (which is a straight line), start with any two points in cartesian space. Using a compass […]