Since the mid-20th century, the hyperbolic paraboloid surface has been one of the most popular mathematical forms for architects. Named Hypar in short, this is the Quadric Surface equation of the Hyperbolic Paraboloid. Erik Demaine summarizes several examples from architecture such as the roof of the Girls’ Grammar School in London (designed by Chamberlin, Powell, and Bonn), the Philips pavilion at the 1958 Brussels exhibition designed by Le Corbusier, and […]
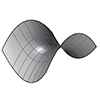
This is another popular “math surface” being rediscovered by designers nowadays, in 2012. Saddle surfaces, seen above as mentioned earlier (here) have a special type named “Monkey Saddle Surface”. This surface was a dramatic example of how Grasshopper can control equations and instantly show graphical results. The mathematical equations start with Z=… this makes it very easy for us to transform any x-y grid centers (a 2d data tree of […]
This is a basic formation of component-based design in a dataflow environment. A double-curved surface is subdivided and re-constructed using straight sections. Parametric model of a surface construction by variable components. The main data list of subsurfaces are distributed into four distinct lists, that will be used to construct lines out of double-curved quadrilateral faces. Such definitions could be further advanced by adding a precise fabrication detail. Parametric definition can […]
