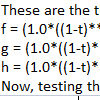Below is the first paper of my son, Mete Yazar. It is about a mathematical and geometric exercise of calculating the surface area of an arbitrary shape (a classical guitar’s body panel). He did a good job in utilizing Bezier/de Casteljau curves and generating the parametric equations of the piecewise curve. I helped him to validate the results by using rhinoceros CAD software. Therefore, it seems that his calculations are […]

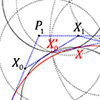
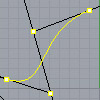
In this short tutorial, I am going to show you how to locate a parametric point on a Bezier curve. This will be a third-degree cubic Bezier curve. So, I start by placing four control points. I name these points from P0 to P3. Then, I connect them by a polyline in order. I explode the polyline into the segments. The parameter of my point must be a number between […]

This is a new paper published in Nexus Network Journal. I tried to implement euclidean constructions by compass in the approximation of famous parametric curves; Bézier curves, and B-Splines. Then, I created the algorithms to calculate the number of steps on a compass-only construction of Bézier curves. I developed a simple Python script to simulate the geometric constructions. However, I have been studying this topic for nearly four years. In […]

Below is the Python code you can run in Rhino, that draws a cubic Bézier curve (degree 3). As you can see, the Rhino Python code is very slow and inefficient because we calculate every point with lots of computations. Instead, we can use the spline formulae to make this quicker but I wanted to show that the mathematical construction is parallel to the geometric one. This is a nested […]

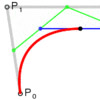
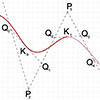
Today’s curve is the beautiful Bezier curve. A series of linear interpolations between the coordinates of control points describe a Bezier curve. So, I created a simple tool in Grasshopper called Bezier Function Extractor to experiment with this elegant construction. In the linear form (degree 1) the linear interpolation between 2 points (P1 and P2). The point at parameter t (0<= t <= 1); Q = tP1 + (1-t)P2. In […]

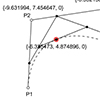
The parametric curve equations are good examples to demonstrate the bridge between computer-aided design and mathematics. Although useless and pointless, it is a good exercise to extract the curve equations. In this Rhino Python code, I present a generalized equation extractor for Rhino. Rhino curves are good examples de Casteljau and Bézier curves. You can see the mathematical underpinnings of Rhino curves with this exercise: This code asks the user […]

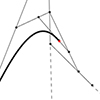
I realized this method of constructing basis splines from given control points while searching for a way to teach students about basis splines. I couldn’t find an easy and visual method to create clamped basis splines by connecting simple cubic Bézier spans. It is a tough job and requires lots of complex equations. However, I suddenly realized that there is a special way of doing that. So I decided to […]

This is a short video tutorial on the B-Spline decomposition I studied earlier here. This tutorial demonstrates how to decompose a B-Spline curve into Bezier curves using Rhino. Despite the original Bezier-de Casteljau algorithm requiring degree+1 control points, Rhino allows drawing a degree-3 curve with any number of control points. By examining knot points and dividing segments appropriately, the B-Spline curve can be manually subdivided into Bezier curves. This involves […]

De Boor’s algorithm, a maestro of basis spline refinement, meticulously navigates through knots, unraveling the intricacies of B-splines with mathematical precision. Meanwhile, De Casteljau, the geometric orchestrator, takes center stage in the Bezier ballet, elegantly guiding control points through a recursive dance. Together, these algorithms fuse art and mathematics, seamlessly sculpting curves and splines with technical finesse, creating a harmonious symphony of numerical intricacies in computational geometry. ChatGPT is so […]

I developed this code 13 years ago while learning the fundamentals of Visual Programming in Grasshopper. I was studying the ways of NURBS curve geometry. The animation shows the construction process of several Bezier Curves. In 2024, I optimized the code and added the thickness. The Flow Earring project showcases the beauty of parametric curves. The Grasshopper definition displays the animated construction process and the variations. The flow of the […]

We’ll use the “Animate” function in Grasshopper3D to create a stop-motion animation. First, you need to determine the parameters you’ll animate, which means defining maximum-minimum values of it. In our example, we’ll be using a simple bezier curve generation algorithm. You can download it here [2011_12_21_bezier curve.ghx]. In this definition, we plan to animate one parameter which is the value of “t” between 0.0 to 1.0. This single change affects various […]

The regular component design technique can be further improved by adding several manipulations. The purpose of this study was to create a surface component that reacts to an inherent parameter (actually a geodesic curve on the surface). However, within the process of parametric modeling, diverse formal potentials emerged. Most interesting results are achieved by adding a graph parameter to control the waves of reaction while splitting the surface as stripes. […]