Not all of them, but when you get the idea, you’ll see there are lots of different alternatives for creating Fuller’s famous Geodesic Domes (Although in fact, he is not the inventor of it). I was playing with Platonic Solids in Rhino and realized that the “Pull” command is very useful in subdividing objects. I modeled this in Rhino 4. First, take a regular Icosahedron and divide it. Because, this is the simplest way for modeling a Geodesic sphere, by creating two kinds of struts (not all of the struts are equal). You can check this post for modeling an Icosahedron. Then, we triangulate and normalize the faces (pulled onto the bounding sphere). Here is an animation of this process:

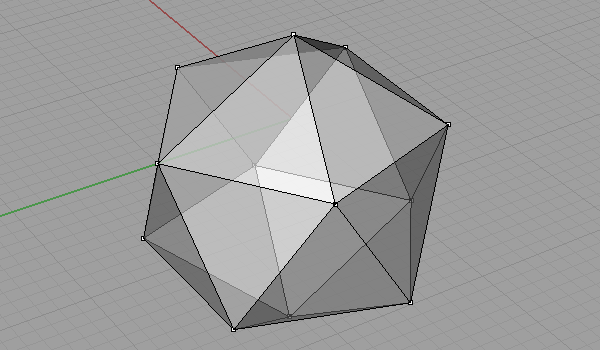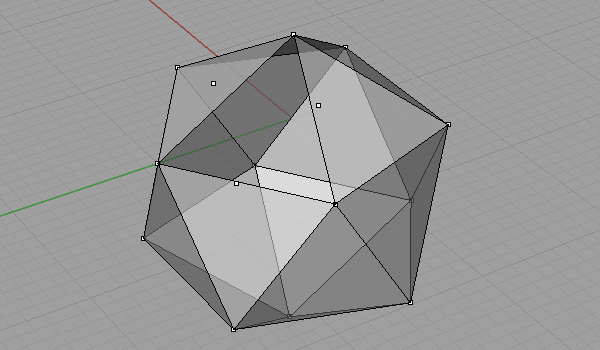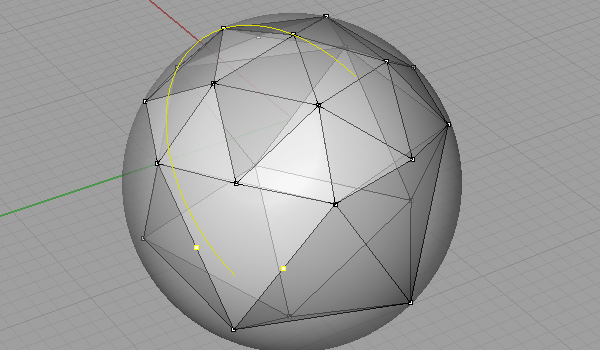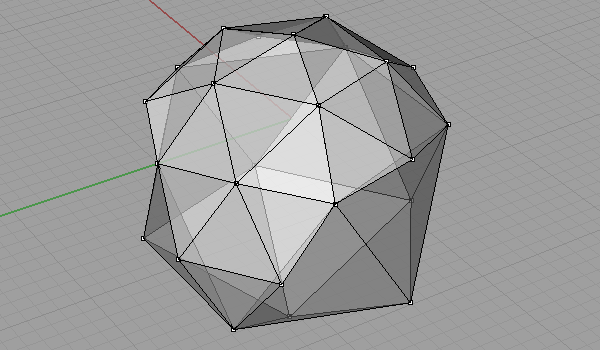
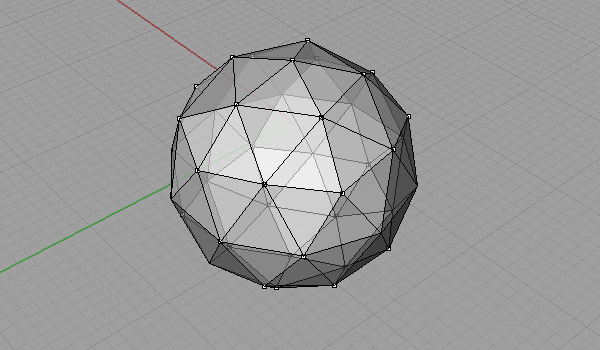
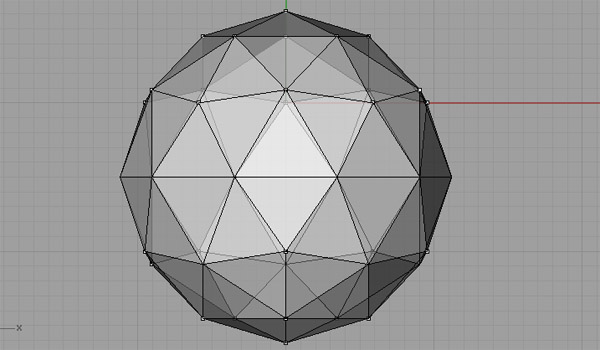
This website is full of details and alternatives to this interesting practice of modeling a Geodesic Sphere.

“…Now, also, to introduce another principle, which is dealing in great circles and spheres, and the word GEODESIC. Geodesic means the most economical relationship between events between any two events. The great circles on spheres are geodesics. There is a shorter distance between any two points on a sphere on the great circle than there is on any of the lesser circles. A great circle is defined as a line formed on the sphere by a plane going through cutting through the center of the sphere. The equator is just such. Each of the planes of longitude goes through the center of the sphere so those are great circles…”

Buckminster Fuller, “Everything I Know”, Session 2, Part 6

If you liked this content and want to download the Rhino file; would you consider being my Patreon? Here is the link to my Patreon page including the working Rhino file for the Geodesic Sphere.