Below is the first paper of my son, Mete Yazar. It is about a mathematical and geometric exercise of calculating the surface area of an arbitrary shape (a classical guitar’s body panel). He did a good job in utilizing Bezier/de Casteljau curves and generating the parametric equations of the piecewise curve. I helped him to validate the results by using rhinoceros CAD software. Therefore, it seems that his calculations are correct.

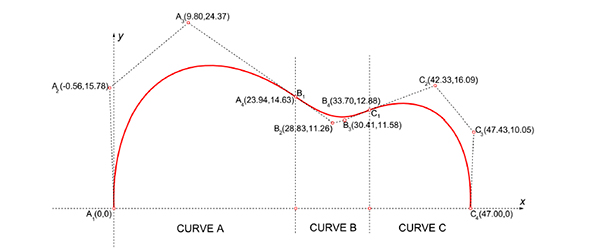
In this paper, we attempted to calculate a guitar’s surface area via bezier curves. The construction of Bezier curves is based on a series of linear interpolations. This gives the utility to express any Bezier curve in terms of parametric polynomials. Thus, this study demonstrated that three third-degree curves are sufficient to approximate the curved shape of a guitar body. The functions derived from this approximation give us the fundamental algebraic definition. Thus one can draw the shape with the help of these functions. The inspiring part of this study is that the mathematical explanation of curve shapes is strongly related to the developments in technology and engineering. Because this eliminates the need for physical templates or blueprints.

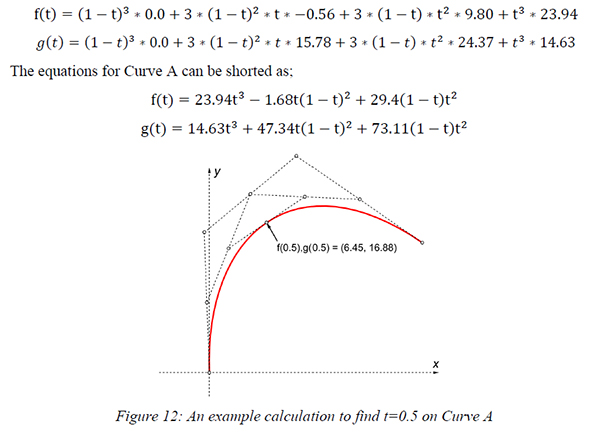
Calculating a guitar’s surface with Bezier curves was an efficient way to analyze these shapes. These curves are widely used in computer-aided design because a designer can draw and transform any curve easily and visually by placing control points. The designers don’t have to know the mathematics behind these curves focusing on their work. However, in this study, we explained these mathematical underpinnings to express this hidden relationship between mathematics and design.