A dodecahedron is a three-dimensional polyhedron with twelve flat, regular pentagonal faces, twenty vertices, and thirty edges. It is one of the Platonic solids and is highly symmetrical, with each face being a regular pentagon. The dodecahedron’s shape is unique among the Platonic solids because its faces are polygons with five sides, unlike the others which have triangular faces. Due to its symmetry, the dodecahedron has been used in various […]
December 2024
An icosahedron is a three-dimensional polyhedron with twenty triangular faces, twelve vertices, and thirty edges. It is one of the five Platonic solids and is highly symmetrical, with all faces being equilateral triangles. A regular icosahedron has equal edge lengths and angles between its faces, making it one of the most symmetrical shapes in three-dimensional space. In this short tutorial video, I am modeling and unrolling an icosahedron. I studied […]
An octahedron is a three-dimensional polyhedron with eight triangular faces, six vertices, and twelve edges. It is one of the Platonic solids and has high symmetry, with all of its faces being equilateral triangles. A regular octahedron can be visualized as two pyramids joined at their bases. It has the same number of faces as a cube has vertices, and the same number of vertices as a cube has faces. […]
A tetrahedron is a three-dimensional shape with four triangular faces, four vertices, and six edges. It is the simplest polyhedron and, in its regular form, has equilateral triangles as faces, with all edges of equal length. Thus, known as one of the Platonic solids, a regular tetrahedron is highly symmetrical, and its shape is considered stable and efficient in many natural and man-made structures. In this short tutorial video, I […]
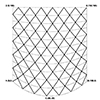
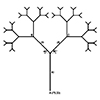
Lattice deformation in parametric design refers to the process of manipulating a grid or mesh structure so that it changes shape in response to specific inputs or parameters. We use this approach widely in computational design for creating complex, organic forms and adaptive systems. Also, lattice deformation can be applied in architectural facades, structural systems, and product design where adaptability and aesthetic fluidity are desired. In this short tutorial video, […]
Parquet deformation refers to a transformation technique applied to a grid or tiling pattern, particularly one that resembles traditional parquet flooring, to create visually interesting and dynamic patterns. This concept is used in parametric design to alter repeating geometric tiles, producing effects such as warping, bending, or otherwise deforming the original pattern while maintaining an overall cohesive layout. In this short tutorial video, I am explaining the drawing of Crosswise […]
Using a compass and straightedge enables precise geometric constructions, allowing for the creation of complex tessellations. To begin these constructions, a single starting point is sufficient. Circles, which represent a collection of points at a specific distance from the center, and straight lines, which represent a collection of points in a particular direction, are utilized for geometric constructions. In this short tutorial, we move on with the beginner-level drawing exercises. […]
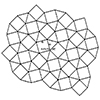
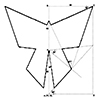
Escher tilings, inspired by the work of Dutch artist M.C. Escher, are inspiring tessellations that cover a plane using repeated geometric shapes without gaps or overlaps. He often used interlocking, recognizable figures like animals and birds to create these patterns, blending art with mathematical precision. His tilings explore symmetry, transformations, and the interplay between two- and three-dimensional space. Escher’s work has influenced both artistic and mathematical fields, particularly in the […]
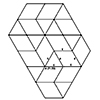
Snub Square Tiling is a semi-regular tessellation of the plane, composed of two squares and three regular triangles at each vertex. The arrangement of these two regular shapes seamlessly covers the plane without any gaps or overlaps. It is one of the eight semi-regular tessellations known in geometry. The dual of Snub Square Tiling is Cairo Pentagonal Tiling, which we will explore later. In this short tutorial, I am drawing […]
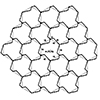
In Japanese, “kagome” refers to basket weaving, and the name of this tiling derives from the traditional basket-weaving craft of Japanese culture. In geometry, we know Kagome tiling as a semi-regular tessellation, Tri-Hexagonal Tiling. This tiling is composed of regular hexagons and triangles that cover the plane completely without gaps or overlaps. The dual of this tiling is the Rhombille Tiling. In this short tutorial, I am explaining the drawing […]
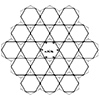
The term “hexa” generally refers to the number six, derived from the Greek word. It is commonly used in mathematics, geometry, and other scientific fields to indicate six-sided shapes or structures. A hexagon is a polygon with six sides and six angles. It is one of the regular polygons, meaning all of its sides and angles are equal. A hexahedron is a polyhedron with six faces. The most well-known example […]
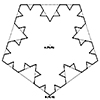
The Koch pentagon is a fractal shape that starts with a regular pentagon. Here, we divide each side of the pentagon into three equal parts. Then, we replace the middle with two sides of an outward-pointing equilateral triangle. We repeat this process for every new side in each iteration, creating a self-similar pattern. Helge von Koch (1870–1924) was a Swedish mathematician known for his analysis and number theory work. He […]
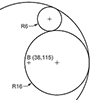
In geometry, “tangent” refers to a scenario where a line, curve, or surface touches another at exactly one point without crossing or leaving a gap. A tangent line to a circle is a straight line that touches the circle at only one point, and it is perpendicular to the radius at that point. Two circles can be tangent either internally or externally. Geometric constructions using a compass and straightedge can […]
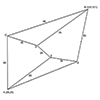
The geometric shapes constructed using only a compass and straightedge have significantly influenced the development of reasoning and logic that underpin modern science. This non-numerical approach is also known as the Synthetic Geometry. Before René Descartes introduced Analytic Geometry, this method was widely studied and practiced. In “Elements”, Euclid explores fundamental rules, such as ‘The straight line between two points is the shortest,’ and derives all geometric truths from simple, […]
The practical geometry of the ancient Egyptian “rope-stretchers” delineated land after the annual flooding of the Nile River. Thus, the term “geometry” derives from the Greek words “gaia” (earth) and “metria” (measurement). Greek mathematicians used compass and straightedge to perform similar calculations on paper. This abstract thinking allowed for insights into the underlying logic, independent of the accuracy of hand tools. So, the abstract “circle” and “line” constructed by perfect […]
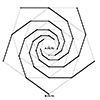
A spiral is a curve that begins at a central point and continuously moves outward, either getting larger (in an outward spiral) or smaller (in an inward spiral). It often revolves around a central point or axis. Spirals are fascinating because they appear in many aspects of nature, mathematics, and art. In this drawing exercise, I utilized several commands to draw such a system. However, this drawing is not a […]
A fractal is a complex geometric shape that we can split into parts, each of which is a reduced-scale copy of the whole. This property is self-similarity. Fractals often exhibit patterns that repeat at different scales. We can find fractals in nature, such as in snowflakes, mountain ranges, trees, and clouds. We can also generate them mathematically. Fractals have applications in various fields such as physics, biology, and computer graphics. […]
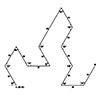
In mathematics, “curve” describes one-dimensional objects or line shapes, regardless of their curvature. Straight lines, polylines, and curved lines all fall under the category of “curves.” You may remember working with equation graphs in high school math classes. For instance, a first-degree equation produces straight-line graphs, while higher-degree equations, like “x squared,” create curved graphs. In this context, we focus on degree-1 curves, drawing straight-line segments using the polyline command. […]
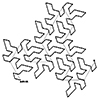
The Flowsnake, or Gosper curve is a space-filling fractal. It is also known as the Peano-Gosper curve. There are other similar space-filling fractals such as the Dragon curve, or the Hilbert curve. A space-filling fractal is a special type of curve, that fills a plane when iterated infinitely. This means, that if you continue to replace every segment of the polyline with the whole drawing, it will quickly become very […]
In computer-aided design (CAD), a polyline is a series (or a chain) of straight lines. Each straight section of a polyline is a “segment,” and the points where the segments connect are “vertices.” If a polyline’s starting and ending vertices coincide, it is a “closed polyline” or a “polygon”. If they do not, the polyline is classified as an “open polyline.” Polylines can be planar (2D) or 3D. The Gosper […]