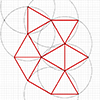
The snub square tiling is one of the semi-regular tessellations, where regular triangles and squares match perfectly to fill the plane without gaps or overlaps. The Euclidean construction of Snub Square tiling is possible by utilizing the basic compass and straightedge operations. I made this construction in Rhinoceros to show that there is no need for any numerical input to locate the points and draw the tiling. There are two […]

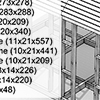
This work emerged out of necessity. In the design and application process of wooden frame structures, where we put thousands of pieces together like a puzzle, the issue of preparing and updating quantity and measurement lists requires the most effort. Hours spent on this and the possibility of making mistakes are very high. However, with the Quantity Surveyor I developed in Grasshopper, you can generate measurement lists almost in real-time. […]

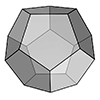
The regular dodecahedron is one of the five Platonic solids, characterized by having 12 regular pentagonal faces, 20 vertices, and 30 edges. When you elongate it, you extend its structure in one or more directions, resulting in a shape that retains the basic properties of the dodecahedron but is stretched out. The elongated dodecahedron might not catch your eye at first—it’s just a long version of a shape you’ve probably […]

Today’s computational curve is the beautiful Sierpinski Triangle. It is a fractal named after the Polish mathematician Waclaw Sierpinski, who described it in 1915, though it had been previously described by other mathematicians. It is a self-replicating pattern that arises from a simple recursive process. To construct the fractal, you start with an equilateral triangle and then repeatedly remove smaller equilateral triangles from its interior, leaving holes. Each iteration involves […]

Villa Savoye is an iconic modernist villa in Poissy, France, built between 1928 and 1931. It was designed by the pioneering Swiss-French architect Le Corbusier, often considered one of the most influential architects of the 20th century. Villa Savoye is a masterpiece of the International Style, embodying the principles of modern architecture that prioritize functionality, simplicity, and the use of new materials such as reinforced concrete. I made this digital […]

This is a 3d modeling tutorial for the platonic solid of dodecahedron. Modeling a dodecahedron is a good exercise for the basic transformation commands such as Rotate3D in Rhinoceros. You will see that it is possible to calculate the rotation angle by using sphere intersections. I learned this elegant method while teaching Architectural Geometry classes 12 years ago. It is based on the fact that, given a rotation axis and […]

The rhombic dodecahedron is a polyhedron with twelve rhombus-shaped faces, where each face has four sides of equal length. It is possible to construct the space-filling variant of the rhombic dodecahedron by arranging multiple such rhombic dodecahedra in a regular pattern so that they fill space without leaving any gaps. In his 1611 work on snowflakes titled “Strena seu de Nive Sexangula,” Johannes Kepler observed that honey bees utilize the […]

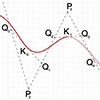
Lissajous curves, named after the French physicist Jules Antoine Lissajous are a family of curves that emerge from the interaction between two harmonic oscillations. They have applications in various fields including physics, engineering, and signal processing. They are commonly used in electronic devices such as oscilloscopes to visualize the phase relationship between two oscillating signals. Similarly, they are also useful in mechanical engineering for analyzing and designing mechanisms that involve […]

This is a short video tutorial on the B-Spline decomposition I studied earlier here. This tutorial demonstrates how to decompose a B-Spline curve into Bezier curves using Rhino. Despite the original Bezier-de Casteljau algorithm requiring degree+1 control points, Rhino allows drawing a degree-3 curve with any number of control points. By examining knot points and dividing segments appropriately, the B-Spline curve can be manually subdivided into Bezier curves. This involves […]

In this short tutorial, I am going to show you how to locate a parametric point on a Bezier curve. This will be a third-degree cubic Bezier curve. So, I start by placing four control points. I name these points from P0 to P3. Then, I connect them by a polyline in order. I explode the polyline into the segments. The parameter of my point must be a number between […]