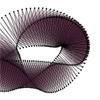
The Möbius strip is a famous mathematical object. Although being in three-dimensional space, it is a closed-loop of only one surface and only one edge. This quality alone makes the object an interesting study for computational design. I aimed to create an object to test our new CNC machine. I wanted to test the egg-crate interlocking fabrication method. This is why the study became a Möbius strip fabrication. Apart from […]

This is not to explain the method of the Parquet Deformation but to see the potential. After we’ve studied regular, semi-regular, dual, and truncated tessellations with students, the Architectural Geometry course expects them to develop a Parquet Deformation handmade such as those shown below. I call them Parquet Deformation handmade. Because they are manually designed but drawn using traditional CAD. The samples you see below are from this website. It […]

Nowadays I plan to enter Rhinoscript, Python, and DesignScript back again. However, I can’t leave Grasshopper3D without mentioning the “cognitive shift” it pioneered in the design computing community. Here is a phrase from a famous special issue of “Computer” Journal, published in 1982 with Tilak Agerwala and Arvind’s editorials; Data flow languages form a subclass of the languages which are based primarily upon function application (i.e., applicative languages). By data […]

This is a late update for my 2012 study on Cairo Pentagonal Tiling (or Cairo Tessellation). Originally, it was an exercise of dual tessellations. Because this tiling is the dual of the famous semi-regular tessellation of Snub Square. After coding the Snub Square tiling, I attempted to generate the dual of it. However, that created an inefficient result. This latest version generates the original Snub Square and Cario Pentagonal Tilings. […]

Here is the step-by-step generation of the old Snub Square Tiling. Frankly, this is the first step in the generation of Cairo Pentagonal Tiling I generated with Grasshopper earlier. Because Cairo pentagonal is the dual of a snub square. The first step was easy. Just dispatch cells of a square grid, then evaluate them according to the ratio of 0.366 approx. which is derived from the bisector of an equilateral […]

The intricate harmony of the Islamic Patterns is amazing. The geometry of this and other Islamic pattern designs are explained in the 3rd chapter of Craig S. Kaplan’s Ph.D. dissertation. I constructed a semi-regular tessellation, particularly the 4.8 because it seems to open interesting explorations that mostly emerge from truncated squares. We know equilateral triangles and hexagons are also fundamental shapes for this task. However, the dual nature of the […]

In 1982, it has been more than 15 years since the dataflow approach to algorithm designing are discussed in computer science. Computer journal publishes a special issue with the foreword of Tilak Agerwala; he says; …We have discussed two characteristics of the von Neumann model of computation: global updatable memory and a single program counter. It will become clear shortly that the data flow model has neither of these. First, the data flow model […]

This was my old plan to work with images in Grasshopper. Certainly, that was not the result I expected, but this could be counted as a starting point. After seeing beautiful circle packing compositions here, I decided to program Grasshopper, so that it’ll create a subdivision, based on image data. This was the initial version, just subdividing a plane with Voronoi points and visualizing it according to the image’s color […]

Today’s fractal is the famous Mandelbrot Set. The Mandelbrot set is a well-known and complex mathematical set often associated with fractals and chaos theory. Named after the mathematician Benoît B. Mandelbrot, it’s a set of complex numbers defined by a simple iterative process. The Mandelbrot set is an intricate and self-similar boundary, which reveals increasingly complex patterns at different magnifications. On the other hand, I heard the term “The fingerprint […]

Today’s fractal is the Julia Set, the amazing simplicity of chaos. There are lots of applets and articles on the internet about this fractal. You can generate this with the iteration of a basic function many times and placing points on the complex plane. I developed a Grasshopper implementation in 2012. Also, this was my first study on complex numbers. At each iteration, the detail level increases. I utilized a […]

Studying circle packing led me back to my high school days. First, I’ve tried to write a vb.net component so that I would say Grasshopper to place circles and check lots of things iterating again and again. Then I felt that this was not my real interest in circle packing. After finding an old post by Daniel Piker (here),  I’m truly enlightened about an old topic of our high school […]

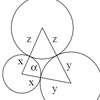
When I was younger, among the branches of philosophy, I had studied a little logic and, among the subjects of mathematics, geometrical analysis and algebra, three arts or sciences which looked as if they ought to contribute something to my project. But in looking at them, I took care, because, so far as logic is concerned, its syllogisms and most of its other instructions serve to explain to others what […]

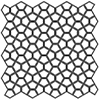
Since last week, I’m very curious about circle packing. There are a couple of complete solutions on the internet. I’m still in the early steps of such a solution yet. A full circle packing means that it does not include any gaps and each circle is tangent to all possible neighbors. Sounds easy in Grasshopper but I couldn’t see any solution yet. There are some circle-packing attempts but they have […]