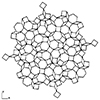
An aperiodic tiling is a pattern that covers the plane without ever repeating itself (i.e., it is non-periodic). A few special shapes, arranged according to specific rules, can cover the entire plane, but the resulting pattern never repeats exactly. I embarked on a 3-day coding sprint to create a general-purpose script in Grasshopper that could generate these tilings. I set Socolar Tiling as my first target. This link contains great […]
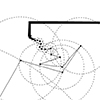
The Fourier Transform is a powerful mathematical technique that allows us to analyze the different frequency components within a signal or shape. Its discrete version, the Discrete Fourier Transform (DFT), is used when working with numerical data. I studied the Fourier Series here before. One of the most fascinating aspects of the DFT is that it can represent a signal or shape using rotating circles (or vectors). Each circle corresponds […]
In large-scale projects, calculating tiling layouts for wall, floor, and ceiling surfaces becomes even more critical. Evolutionary optimization of tilings is a viable approach. Considering how time-consuming and labor-intensive this process can be, I considered using Galapagos, an old but often overlooked feature in Grasshopper, which might be particularly useful here. Galapagos provides an alternative interface for evolutionary optimization within Grasshopper. It works by minimizing or maximizing a fitness value […]
Although it appears simple, Goldberg Polyhedra in Grasshopper became a tough challenge, which I like. I spent about 24 hours attempting to generate these. I started with Goldberg’s original method. This creates an equilateral triangle using coordinates denoted as m and n on a hexagonal grid. Then, we place this triangle onto the faces of an icosahedron. Finally, we project them onto a concentric sphere. We can create many polyhedra […]
The Hilbert Curve is one of the results of David Hilbert’s vision of mathematics as a network of symbolic systems. Defined in 1891, this curve is a fractal that fills a two-dimensional plane with a one-dimensional line in the limit. It exhibits self-similarity. It emerged from representing higher-dimensional spaces through continuous, lower-dimensional entities. A curve that grows within a bounded area remains continuous but non-differentiable. Yet it possesses infinite length. […]
I had been researching Goldberg Polyhedra for a while. While exploring how to perform chamfer operations in Grasshopper, I found some interesting results. I want to share them with you. In this Grasshopper project, I reused my previous work, where I built a dodecahedron using the golden ratio. Essentially, all I did was add the Fillet Edge component. I don’t use this component much, so I learned it through this […]
Robotic EarthCrafts II occurred in the summer of 2024 at Istanbul Bilgi University, seven years after the first. Together with Fulya Özsel Akipek, Nilüfer Kozikoglu, Abdullah Mallah, and Halit Mallah, we experimented with the robotic fabrication of molds for rammed-earth structures. The focus shifted toward a human scale based on the experience gained from Robotic EarthCrafts I. At the workshop’s core were spatial systems resembling muqarnas, which incorporated non-planar geometric transitions. Unlike the first workshop, […]
3D printing, also known as additive manufacturing, is a process of creating three-dimensional objects from a digital file by building them layer by layer. Unlike traditional manufacturing, where the material is cut or molded into shape, 3D printing adds material in successive layers. This allows for greater precision and the creation of complex geometries. In this short tutorial video, I am using Cura software to slice a simple geometry for […]
Relief in the context of art and sculpture refers to a technique where a three-dimensional form is created on a flat surface. The object or figure “protrudes” from the background, creating depth and texture. In this short tutorial video, I am modeling waves relief using the basic drawing and modeling commands of the Rhinoceros software. Here, I use the point surface command. Because, in Rhinoceros, generally we describe the parametric […]
Truchet patterns refer to a set of geometric designs based on simple, repeating shapes, usually tiles or squares. These tiles can be rotated or flipped to create complex and visually interesting patterns. A French mathematician, Michel Truchet introduced these patterns in the 1970s. Since then, you can see them often in art, design, and mathematics. In this short video tutorial, I am modeling truchet relief in Rhinoceros CAD software. My […]
A “hypar” is short for a hyperbolic paraboloid, a double-curved, saddle-shaped surface often used in architecture and structural design due to its unique geometric properties. It is a ruled surface, meaning it can be constructed entirely with straight lines, despite its curved appearance. In this short tutorial video, I am building a beginner-level 3D pattern that resembles the hypar surface. This is a basic drawing exercise to control the viewport […]
In art, design, and geometry, folding involves bending or creasing a material—such as paper, fabric, or other flexible substances—into defined shapes or patterns. Folding techniques can also be used to create multidimensional forms and structures, blending artistic expression with practical functionality. In this short tutorial video, I am modeling a folds relief pattern. This pattern stands out due to its resemblance to a collapsible folding system, combining both structural and […]
In geometry, a truncated icosidodecahedron, rhombitruncated icosidodecahedron, great rhombicosidodecahedron, omnitruncated dodecahedron, or omnitruncated icosahedron is an Archimedean solid. It is one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces. In this short tutorial, I am constructing an irregular truncated icosidodecahedron. It is not the regular Archimedean solid, but a rough approximation of it. I made this model to exercise the exploration of […]
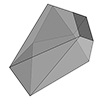
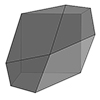
The sphenoid hendecahedron is a unique and interesting polyhedron. As the name implies, a “hendecahedron” is a polyhedron with 11 faces, while “sphenoid” refers to a specific type of shape that is often unusual, asymmetrical, and typically wedge-shaped. This polyhedron fills space, packing 3D space without gaps or overlaps. Its convex shape allows it to tessellate efficiently. Therefore, space-filling polyhedra play a crucial role in understanding tessellations and geometric arrangements, […]
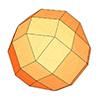
The rhombicosidodecahedron, an Archimedean solid, is one of the 13 convex polyhedra made up of regular polygons. While all its faces are congruent, they consist of various types of regular polygons. I previously explored this fascinating polyhedron and am revisiting it now as part of the Architectural Geometry course. In this short tutorial video, I demonstrate the modeling of a rhombicosidodecahedron. Despite its lengthy and unusual name, this polyhedron is […]
The Herschel nonahedron is a canonical polyhedron whose skeleton is the Herschel graph. It has 11 vertices, 18 edges, and 9 faces. Of the edges, 6 are short and 12 are long. It is characterized by having nine faces (hence the prefix “ennea” meaning nine in Greek). In this short tutorial video, I am folding Herschel’s enneahedron. To do that, I am constructing the interior angles of this polyhedron using […]
In geometry, the excavated dodecahedron is a star polyhedron that looks like a dodecahedron with concave pentagonal pyramids in place of its faces. In this short tutorial video, I am modeling an excavated dodecahedron in the Rhinoceros software. I use basic drawing and modeling commands. I aim to introduce this skill to beginner-level architects and designers. As the name suggests, this process includes the construction of the dodecahedron first. Then, […]