Today’s fractal is the famous Mandelbrot Set. The Mandelbrot set is a well-known and complex mathematical set often associated with fractals and chaos theory. Named after the mathematician Benoît B. Mandelbrot, it’s a set of complex numbers defined by a simple iterative process. The Mandelbrot set is an intricate and self-similar boundary, which reveals increasingly complex patterns at different magnifications. On the other hand, I heard the term “The fingerprint of God” in some sources resembling its aesthetic and philosophical essence. This Grasshopper definition is generating points of this set with a given escape value. It is fun to play with it. But be careful, if you increase the number of points too much, it may crash your computer.

This Grasshopper definition generates approximations of the Mandelbrot Set. I created the parametric model in Grasshopper with native components. Thus, no add-ons are necessary for it to work. There is one VB.net script that is responsible for the calculations. You can see it above. The output of the model is a set of points. You can use this model further to investigate this fascinating fractal. The inputs are the total number of random points (be careful while increasing this), the escape value, and the number of iterations.

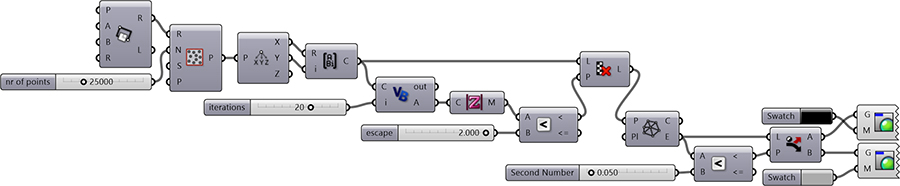
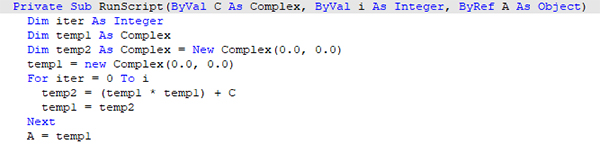
You can regenerate this Grasshopper definition by checking the above images and the code. It is fairly simple for an intermediate Grasshopper user. However, if you like what I do, and want to support me in covering the expenses of web hosting, would you consider being one of my Patreons? Here is the link to my Patreon page, including the Grasshopper definition for the Mandelbrot Set and more. I appreciate your support.