Dodecahedron: Drawing and Unrolling

The dodecahedron is a Platonic Solid with 12 equilateral pentagonal faces. It has a close relationship with its 20-sided dual, Icosahedron. Mete Tüneri showed the following method of Dodecahedron construction, using only distances, corners of the pentagon, and a visionary equilateral triangle underneath.

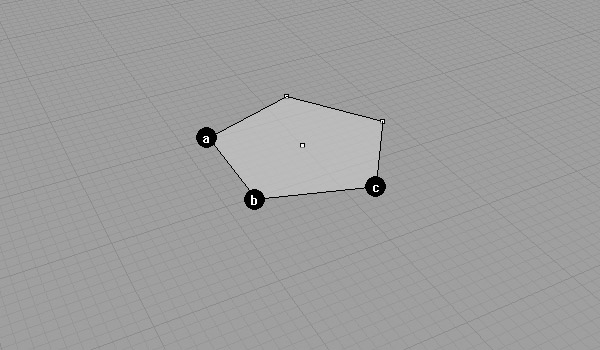
We’ll construct Dodecahedron, assuming that we’ve drawn an initial equilateral pentagon.

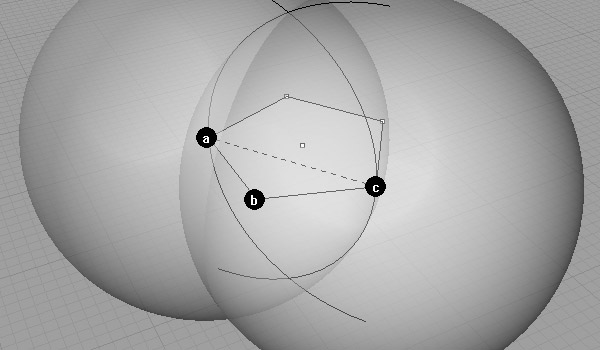
We need to find out the pentagon’s angle of 3d rotation. First, put spheres at points a and c, with a radius of a to c.

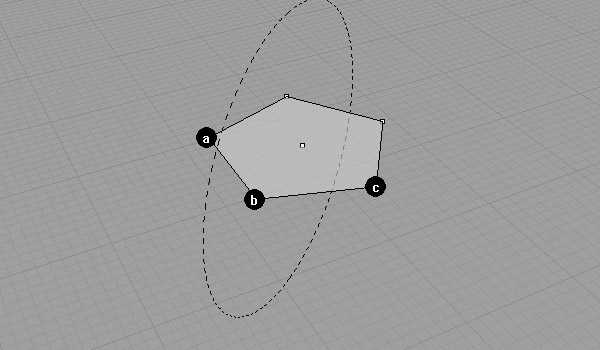
The intersection of these spheres results in a circle. We know that every point on this circle would create an equilateral triangle. But we need one more constraint to find it.

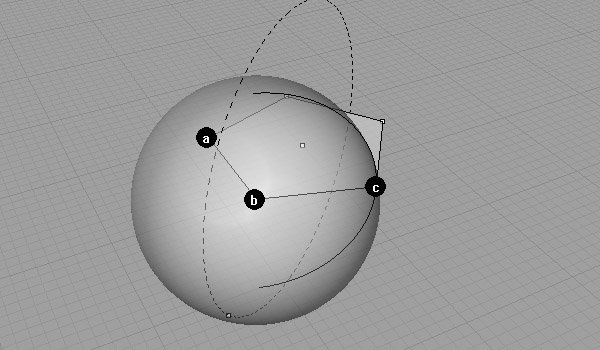
The point, we are searching for also lies at the same distance to b, as it’s equal to ab, or bc. Thus, we’re placing a sphere centered on b and a radius of ab.

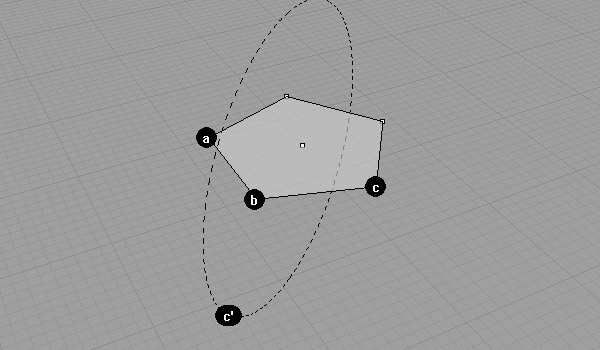
The intersection of the circle and the sphere results in point c’.

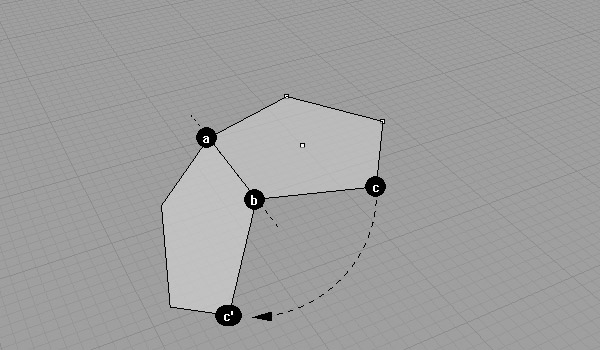
Now, the pentagon’s angle of rotation is found geometrically. I executed a 3d rotation using ab as the rotation axis and c-c’ as the angle.

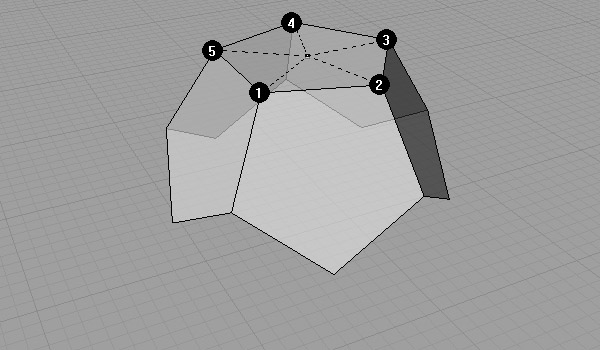
After we finish one face, it’s possible to create others as they are all equal.

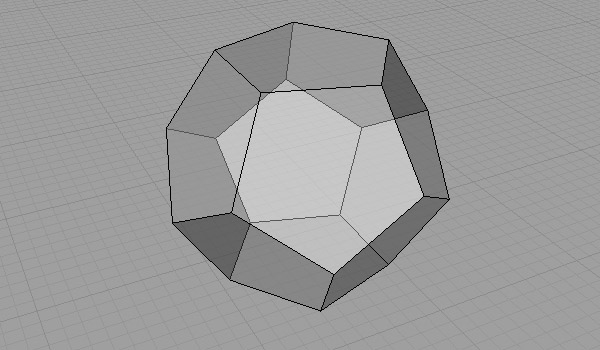
Finally, I finished the bottom part with the same method (or just copying) Dodecahedron.

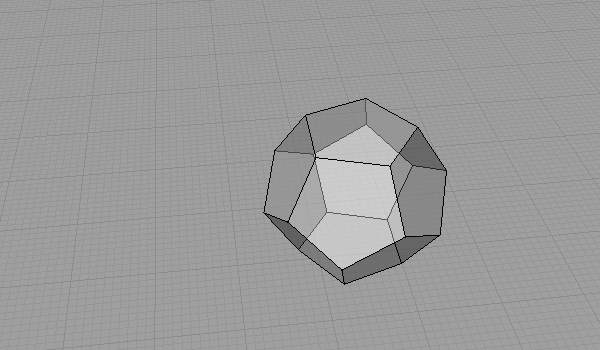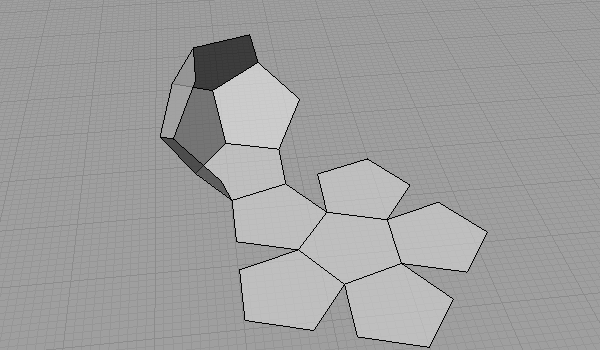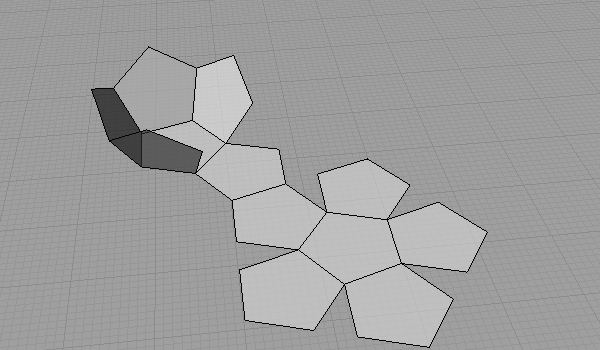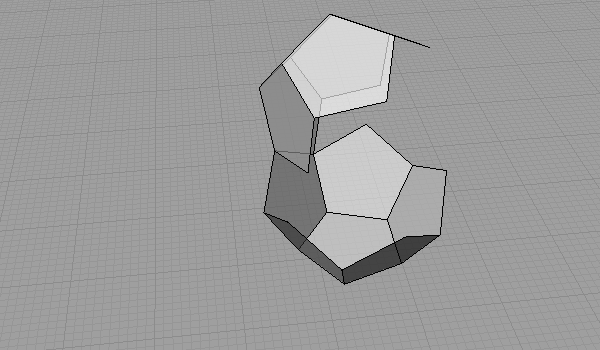
Here is one of the many unrolling sequences of the 12-sided Platonic Solid.

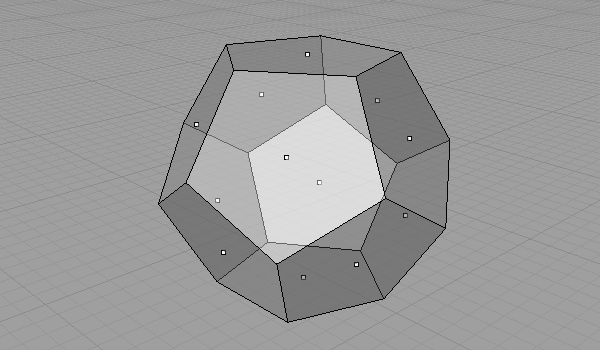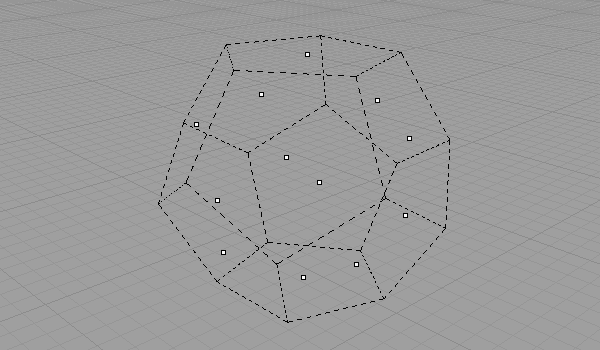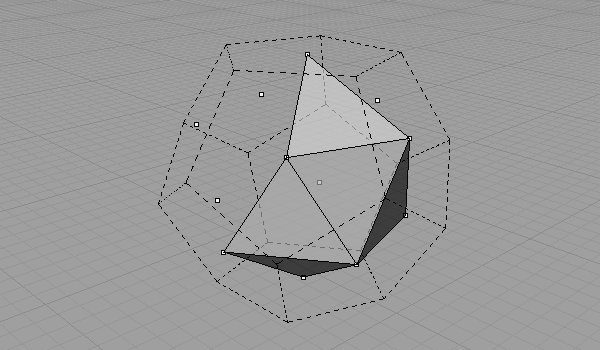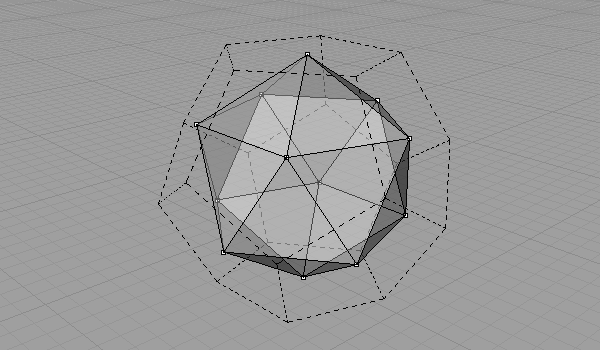
When we connect all face centers of a Dodecahedron, we’ll find its dual, Icosahedron. You can watch the video of this geometric construction on my YouTube channel here.